题目内容
已知一个一次函数 经过
经过 ,
, 两点,求此一次函数的解析式;
两点,求此一次函数的解析式;
 经过
经过 ,
, 两点,求此一次函数的解析式;
两点,求此一次函数的解析式;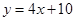
试题分析:根据图象经过
 ,
, 两点即可根据待定系数法求得函数关系式.
两点即可根据待定系数法求得函数关系式.∵一次函数
 经过
经过 ,
, 两点
两点∴
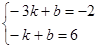 ,解得
,解得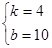
∴此一次函数的解析式为
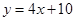 .
.点评:本题属于基础应用题,只需学生熟练掌握待定系数法求函数关系式,即可完成.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
题目内容
 经过
经过 ,
, 两点,求此一次函数的解析式;
两点,求此一次函数的解析式;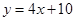
 ,
, 两点即可根据待定系数法求得函数关系式.
两点即可根据待定系数法求得函数关系式. 经过
经过 ,
, 两点
两点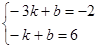 ,解得
,解得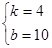
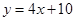 .
.
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案