题目内容
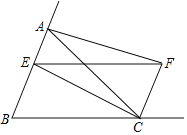
【题目】在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE,垂足为F
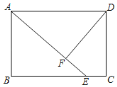
(1)求证:DF=AB;
(2)若∠FAD=30°,且AB=4,求AD.
【答案】(1)见解析;(2)AD=8.
【解析】
(1)利用“AAS”证△ADF≌△EAB即可得;
(2)由∠ADF+∠FDC=90°、∠DAF+∠ADF=90°得∠FDC=∠DAF=30°,据此知AD=2DF,根据DF=AB可得答案.
(1)证明:在矩形ABCD中,
∵AD∥BC,∠B=90°,
∴∠AEB=∠DAF,
又∵DF⊥AE,
∴∠DFA=90°,
∴∠DFA=∠B,
在△ADF和△EAB中,
 ,
,
∴△ADF≌△EAB(AAS),
∴DF=AB.
(2)∵∠ADF+∠FDC=90°,∠DAF+∠ADF=90°,
∴∠FDC=∠DAF=30°,
∴AD=2DF,
∵DF=AB,
∴AD=2AB=8.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目