题目内容
【题目】如图,四边形OABC是矩形,A(2,1),B(0,5),点C在第二象限,则点C的坐标是______.
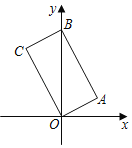
【答案】(﹣2,4)
【解析】
作AM⊥x轴于M,CN⊥y轴于N,则∠AMO=∠BNC=90°,OM=2,AM=1,OB=5,证明△BCN≌△AOM(AAS),得出BN=AM=1,CN=OM=2,得出ON=OB﹣BN=4,即可得出答案.
解:作AM⊥x轴于M,CN⊥y轴于N,如图所示:

则∠AMO=∠BNC=90°,
∴∠AOM+∠OAM=90°,
∵A(2,1),B(0,5),
∴OM=2,AM=1,OB=5,
∵四边形OABC是矩形,
∴BC=AO,∠AOC=90°,BC∥OA,
∴∠CBN=∠AOB,
∵∠AOM+∠AOB=90°,
∴∠CBN=∠AOB=∠OAM,
在△BCN和△AOM中, ,
,
∴△BCN≌△AOM(AAS),
∴BN=AM=1,CN=OM=2,
∴ON=OB﹣BN=4,
∴点C的坐标是(﹣2,4);
故答案为:(﹣2,4).

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目