Question

【题目】如图，在单位长度为1的正方形网格中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格图中进行下列操作（以下结果保留根号）.

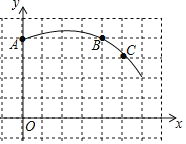
（1）利用网格作出该圆弧所在圆的圆心D点的位置，并写出D点的坐标为　 ；

（2）连接AD、CD，则⊙D的半径为　 ，∠ADC的度数为　 ．

Answer 1

【答案】（1）如图，点D为所作，见解析；D点坐标为（2，1）；（2）⊙D的半径为，∠ADC的度数为90°．

【解析】

（1）利用网格特点，作AB和BC的垂直平分线，然后根据垂径的推论可判定它们的交点为D点，从而得到D点坐标；

（2）先利用勾股定理计算出DA、DC、AC，然后利用勾股定理的逆定理证明∠ADC的度数为90°．

（1）如图， 利用垂径定理可作AB和BC的垂直平分线，两线的交点即为D点，可得出D点坐标为（2，1）；

（2）AD＝，

∵DA2+DC2＝AC2， ∴△ADC为直角三角形，∠ADC＝90°，

即⊙D的半径为，∠ADC的度数为90°．