��Ŀ����
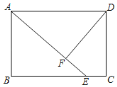
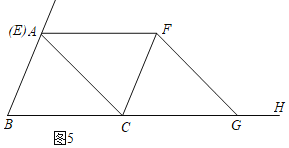
����Ŀ����ͼ���ڵ�����ABC�У�AC��BC��3![]() ��AB��6����E�ӵ�B��������BA��ÿ��3����λ���ٶ��˶�������E��BC��ƽ���߽���ACB�����ƽ����CF�ڵ�F��
��AB��6����E�ӵ�B��������BA��ÿ��3����λ���ٶ��˶�������E��BC��ƽ���߽���ACB�����ƽ����CF�ڵ�F��
��1����֤���ı���BCFE��ƽ���ı��Σ�
��2������E�DZ�AB���е�ʱ������AF�����ж��ı���AECF����״����˵�����ɣ�
��3�����˶�ʱ��Ϊt�룬�Ƿ����t��ֵ��ʹ���ԡ�EFC����������Ϊ���������ƽ���ı���ǡ�������Σ������ڣ������t��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��֤������������2���ı���AECF�Ǿ��Σ����ɼ���������3��t��ֵΪ![]() ���
���![]() ���2��
���2��
��������
��1���ɵ��������ε����ʵã���B=��BAC�����ɽ�ƽ���߶������������ǵ����ʿɽ��
��2������һ������ֱ�ǵ�ƽ���ı����Ǿ��οɽ��
��3���������������EF=CF����CE=CF����CE=EF���ֱ��з��̿ɽ��
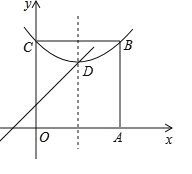
֤������1����ͼ1��
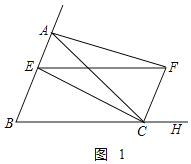
��AC��BC��
���B����BAC��
��CFƽ�֡�ACH��
���ACF����FCH��
�ߡ�ACH����B+��BAC����ACF+��FCH��
���FCH����B��
��BE��CF��
��EF��BC��
���ı���BCFE��ƽ���ı��Σ�
��2���ı���AECF�Ǿ��Σ�
�����ǣ�
��E��AB���е㣬AC��BC��
��CE��AB��
���AEC��90����
�ɣ�1��֪���ı���BCFE��ƽ���ı��Σ�
��CF��BE��AE��
��AE��CF��AE��CF��
���ı���AECF��ƽ���ı��Σ��ҡ�AEC��90����
���ı���AECF�Ǿ��Σ�
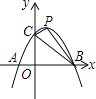
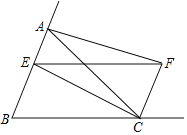
��3������EF��CF����Ϊ�ڱ��������ƽ���ı���ǡ��������ʱ����ͼ2��

��BE��BC����3t��3![]() ��
��
��t��![]() ��
��
����CE��CF����Ϊ�ڱ��������ƽ���ı���ǡ��������ʱ����ͼ3����C��CD��AB��D������GC��

��AC��BC��3![]() ��AB��6��
��AB��6��
��BD��AD��3��
�ɹ��ɶ����ã�CD��![]() ��
��![]() ��6��
��6��
���ı���CEGF�����Σ�
��EF��GC����EF��BC��
��GC��BC���ҡ�EGC����ECG��
���EBC����ECB��
��BE��CE��3t��
�ߣ�3t��2��62+��3t��3��2��
��t��![]() ��
��
����CE��EF����Ϊ�ڱ��������ƽ���ı���ǡ��������ʱ����ͼ4��CA��AF��BC����ʱE��A�غϣ�
��t��2��
����������t��ֵΪ![]() ���
���![]() ���2�룻
���2�룻