题目内容
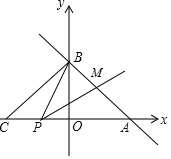
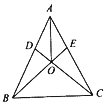
【题目】如图,![]() 中,AB=AC,D、E分别在边AB、AC上,且满足AD=AE.下列结论中:①
中,AB=AC,D、E分别在边AB、AC上,且满足AD=AE.下列结论中:①![]() ;②AO平分∠BAC;③OB=OC;④AO⊥BC;⑤若
;②AO平分∠BAC;③OB=OC;④AO⊥BC;⑤若![]() ,则
,则![]() ;其中正确的有( )
;其中正确的有( )
A. 2个B. 3个C. 4个D. 5个
【答案】D
【解析】
利用SAS可证明△ABE≌△ACD,判断①正确;根据全等三角形的性质以及邻补角定义可得∠BDO=∠BEC,继而利用AAS证明△BOD≌△COE,可得OD=OE,BO=OC,判断③正确;利用SSS证明△AOD≌△AOE,可得AO平分∠BAC,判断②正确,继而根据等腰三角形三线合一的性质可判断④正确,根据三角形的高相等时,两三角形的面积比就是底边之比,通过推导可判断⑤正确.
在△ABE与△ACD中,
 ,
,
∴△ABE≌△ACD,故①正确;
∴∠AEB=∠ADC,
∴∠BDO=∠BEC,
∵AB=AC,AD=AE,∴BD=CE,
在△BOD与△COE中,
 ,
,
∴△BOD≌△COE,
∴OD=OE,BO=OC,故③正确;
在△AOD与△AOE中,
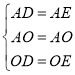 ,
,
∴△AOD≌△AOE,
∴∠DAO=∠EAO,
即AO平分∠BAC,故②正确,
又∵AB=AC,
∴AO⊥BC,故④正确,
∵![]() ,
,
∴S△BOD=2S△AOD,
又∵△BOD≌△COE,
∴S△COE=2S△AOD,
又∵△AOD≌△AOE,
∴S△AOC=3S△AOD,
∴OC=3OD,
即![]() ,故⑤正确,
,故⑤正确,
故选D.

练习册系列答案
相关题目