题目内容
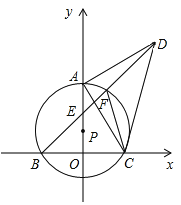
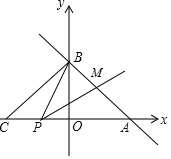
【题目】如图,已知直线y=-![]() x+b与y轴相交于点B(0,3),与x轴交于点A,将△AOB沿y轴折叠,使点A落在x轴上的点C.
x+b与y轴相交于点B(0,3),与x轴交于点A,将△AOB沿y轴折叠,使点A落在x轴上的点C.
(1)求点C的坐标;
(2)设点P为线段CA上的一个动点,点P与点A、C不重合.联结PB.以点P为端点作射线PM交AB于点M,使∠BPM=∠BAC.
①求证:△PBC∽△MPA.
②是否存在点P,使△PBM为直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)C(-4,0);(2)①证明见解析,②存在.使△PBM为直角三角形的点P有两个P1(-![]() ,0),P2(0,0).
,0),P2(0,0).
【解析】
(1)根据B点坐标求得直线解析式,再求得A点坐标,然后根据A与C关于y轴对称,据此即可确定C的坐标;
(2)①根据点C与点A关于y轴对称,即可得到BC=BA,则∠BCP=∠MAP,再根据三角形的外角的性质即可证得∠PMA=∠BPC,从而证得两个三角形相似;
②首先求得B的坐标,当∠PBM=90°时,则有△BPO∽△ABO,根据相似三角形的对应边的比相等,即可求得PO的长,求得P的坐标;
当∠PMB=90°时,则∠PMA═90°时,BP⊥AC,则此时点P与点O重合.则P的坐标可以求得.
(1)解:∵直线y=-![]() x+b与y轴相交于点B(0,3),
x+b与y轴相交于点B(0,3),
∴b=3,
∴直线的解析式为y=-![]() x+3,
x+3,
令y=0,得到x=4,
∴A(4,0),
∵点C与点A关于y轴对称,
∴C(-4,0);
(2)①证明:∵∠BPM=∠BAC,且∠PMA=∠BPM+∠PBM,∠BPC=∠BAC+∠PBM,
∴∠PMA=∠BPC,
又∵点C与点A关于y轴对称,且∠BPM=∠BAC,
∴∠BCP=∠MAP,
∴△PBC∽△MPA;
②解:存在.
由题意:A(4,0),B(0,3),C(-4,0)
当∠PBM=90°时,则有△BPO∽△ABO,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴PO=![]() ,即:P1(-
,即:P1(-![]() ,0).
,0).
当∠PMB=90°时,则∠PMA═90°,
∴∠PAM+∠MPA=90°,
∵∠BPM=∠BAC,
∴∠BPM+∠APM=90°,
∴BP⊥AC.
∵过点B只有一条直线与AC垂直,
∴此时点P与点O重合,即:符合条件的点P2的坐标为:P2(0,0).
∴使△PBM为直角三角形的点P有两个P1(-![]() ,0),P2(0,0).
,0),P2(0,0).