题目内容
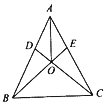
【题目】如图1,已知∠ABC=90°,△ABC是等腰三角形,点D为斜边AC的中点,连接DB,过点A作∠BAC的平分线,分别与DB,BC相交于点E,F.
(1)求证:BE=BF;
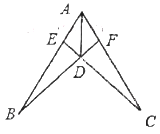
(2)如图2,连接CE,在不添加任何辅助线的条件下,直接写出图中所有的等腰三角形.

【答案】(1)见解析;(2)△ABD、△CBD是等腰三角形,△ABC是等腰三角形,△BEF是等腰三角形.
【解析】
(1)根据直角三角形的性质得到BD⊥AC,∠DBC=45°,根据角平分线的定义得到∠BAF=22.5°,根据三角形内角和定理计算,根据等腰三角形的判定定理证明即可;
(2)根据等腰三角形的概念解答.
(1)证明:∠ABC=90°,BA=BC,点D为斜边AC的中点,
∴BD⊥AC,∠DBC=45°,
∵AF是∠BAC的平分线,
∴∠BAF=22.5°,
∴∠BFE=67.5°,
∴∠BEF=180°﹣∠EBF﹣∠EFB=67.5°,
∴∠BFE=∠BEF,
∴BE=BF;
(2)∵∠ABC=90°,BA=BC,点D为斜边AC的中点,
∴BD=AD=CD,
∴△ABD、△CBD是等腰三角形,
由已知得,△ABC是等腰三角形,
由(1)得,△BEF是等腰三角形,
∵AF是∠BAC的平分线,BD是∠ABC的平分线,
∴点E是△ABC的内心,
∴∠EAC=∠ECA=22.5°,
∴△AEC是等腰三角形.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目