题目内容
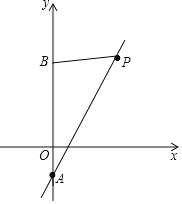
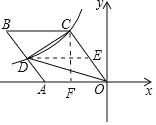
【题目】如图，菱形OABC的一边OA在x轴的负半轴上，O是坐标原点，tan∠AOC=
，反比例函数y=
的图象经过点C，与AB交于点D，若△COD的面积为16，则k的值等于_____．
【答案】
【解析】
易证S菱形ABCO=2S△CDO，再根据tan∠AOC的值即可求得菱形的边长，即可求得点C的坐标，代入反比例函数即可解题．
作DE∥AO，CF⊥AO，设CF=4x，
∵四边形OABC为菱形，
∴AB∥CO,AO∥BC，
∵DE∥AO，
∴∴S△ADO=S△DEO，
同理S△BCD=S△CDE，
∵S菱形ABCO=S△ADO+S△DEO+S△BCD+S△CDE，
∴S菱形ABCO=2（S△DEO+S△CDE）=2S△CDO=32，
∵tan∠AOC=
∴OF=3x，
∴
∴OA=OC=5x，
∵S菱形ABCO=AOCF
,解得：
∴
∴点C坐标为
∵反比例函数
的图象经过点C，
∴代入点C得：
故答案为:
练习册系列答案
相关题目
【题目】已知关于
的代数式
，设代数式
的值．
下表中列出了当分别取-1，0，1，2，3，4，5，…，
，
，…时对应的值．
| … | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
|
| … |
| … | 10 | 5 | 2 | 1 | 2 | 5 |
| … |
|
| … |
（1）表中
的值为 ；
（2）当
时，
有最小值，最小值是 ；
（3）比较
与
的大小．
