题目内容
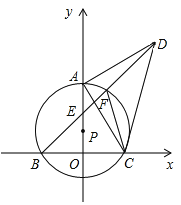
【题目】如图，某新建公园有一个圆形人工湖，湖中心O处有一座喷泉，小明为测量湖的半径，在湖边选择A、B两个点，在A处测得∠OAB=45°，在AB延长线上的C处测得∠OCA=30°，已知BC=50米，求人工湖的半径．（结果保留根号）
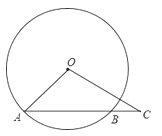
【答案】人工湖的半径为（25
+25
）米．
【解析】
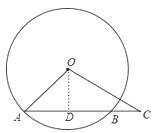
过点O作OD⊥AC于点D，由垂径定理可知AD=BD，根据∠OAB=45°可知AD=OD，设AD=x，则OD=x，OA=x，CD=x+BC=（x+50）米，再根据∠OCA=30°即可得出x的值，进而得出结论．
解：过点O作OD⊥AC于点D，则AD=BD，
∵∠OAB=45°，
∴AD=OD，
∴设AD=x，则OD=x，OA=x，CD=x+BC=x+50）．
∵∠OCA=30°，
∴
=tan30°，即
=
，
解得x=25
+25，
∴OA=x=×（25+25）=（25+25）（米）．
答：人工湖的半径为（25+25）米．
练习册系列答案
相关题目
【题目】已知关于
的代数式
，设代数式
的值．
下表中列出了当分别取-1，0，1，2，3，4，5，…，
，
，…时对应的值．
| … | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
|
| … |
| … | 10 | 5 | 2 | 1 | 2 | 5 |
| … |
|
| … |
（1）表中
的值为 ；
（2）当
时，
有最小值，最小值是 ；
（3）比较
与
的大小．
