题目内容
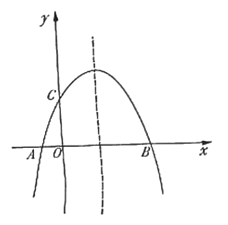
【题目】如图,抛物线y=ax2+bx+c交x轴分别于点A(﹣3,0),B(1,0),交y轴正半轴于点D,抛物线顶点为C.下列结论
①2a﹣b=0;
②a+b+c=0;
③当m≠﹣1时,a﹣b>am2+bm;
④当△ABC是等腰直角三角形时,a=![]() ;
;
⑤若D(0,3),则抛物线的对称轴直线x=﹣1上的动点P与B、D两点围成的△PBD周长最小值为3![]() ,其中,正确的个数为( )
,其中,正确的个数为( )
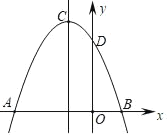
A.2个B.3个C.4个D.5个
【答案】D
【解析】
把A、B两点坐标代入抛物线的解析式并整理即可判断①②;
根据抛物线的顶点和最值即可判断③;
求出当△ABC是等腰直角三角形时点C的坐标,进而可求得此时a的值,于是可判断④;
根据利用对称性求线段和的最小值的方法(将军饮马问题)求解即可判断⑤.
解:把A(﹣3,0),B(1,0)代入y=ax2+bx+c得到![]() ,消去c得到2a﹣b=0,故①②正确;
,消去c得到2a﹣b=0,故①②正确;
∵抛物线的对称轴是直线x=﹣1,开口向下,∴x=﹣1时,y有最大值,最大值=a﹣b+c,
∵m≠﹣1,∴a﹣b+c>am2+bm+c,∴a﹣b>am2+bm,故③正确;
当△ABC是等腰直角三角形时,C(﹣1,2),
可设抛物线的解析式为y=a(x+1)2+2,把(1,0)代入解得a=﹣![]() ,故④正确,
,故④正确,
如图,连接AD交抛物线的对称轴于P,连接PB,则此时△BDP的周长最小,最小值=PD+PB+BD=PD+PA+BD=AD+BD,
∵AD=![]() =3
=3![]() ,BD=
,BD=![]() =
=![]() ,
,
∴△PBD周长最小值为3![]() ,故⑤正确.
,故⑤正确.
故选:D.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目