题目内容
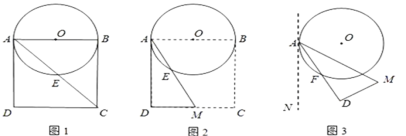
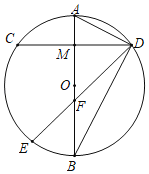
【题目】如图,AB是⊙O的直径,M是OA的中点,弦CD⊥AB于点M,连接AD,点E在BC上,∠CDE=45°,DE交AB于点F,CD=6.
(1)求∠OAD的度数;
(2)求DE的长.
【答案】(1)60°;(2)![]() +3
+3![]() .
.
【解析】
(1)连接OD.证明△AOD是等边三角形即可解决问题.
(2)连接OC,CF,EC.证明△CFD是等腰直角三角形即可解决问题.
(1)连接OD.
∵DC⊥OA,AM=MO,
∴DA=DO,
∵OA=OD,
∴OA=OD=AD,
∴△AOD是等边三角形,
∴∠OAD=60°.
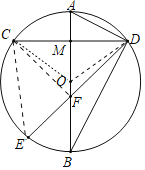
(2)连接OC,CF,EC.
∵OA⊥CD,
∴弧AC=弧AD,CM=DM,
∴∠AOC=∠AOD=60°,FC=FD,
∵∠CDE=45°,
∴CF=DF,FM=CM=DM=3,DF=FC=3![]() ,
,
∵∠CED=![]() ∠COD=60°,∠CFE=90°,
∠COD=60°,∠CFE=90°,
∴EF=![]() CF=
CF=![]() ,
,
∴DE=EF+DF=![]() +3
+3![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目