Question

【题目】已知：如图，在Rt△ABC中，∠C＝90°，Rt△ABC的内切圆⊙O，切点分别为点D、E、F，

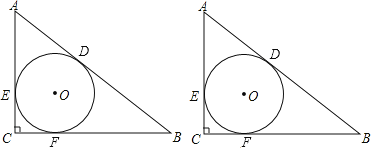
（1）若AC＝3，BC＝4，求△ABC的内切圆半径；

（2）当AD＝5，BD＝7时，求△ABC的面积；

（3）当AD＝m，BD＝n时，直接写出求△ABC的面积（用含m，n的式子表示）为　 　．

Answer 1

【答案】（1）1；（2）35；（3）mn

【解析】

（1）连接OD、OE、OF，如图，设⊙O的半径为r，利用勾股定理计算出AB＝5，利用切线的性质和切线长定理得到OE⊥AC，OF⊥BC，CE＝CF，AE＝AD，BF＝BD，则四边形CFOE为正方形，所以CE＝CF＝OE＝r，从而得3﹣r+4﹣r＝5，然后求出r即可；

（2）设⊙O的半径为r，利用（1）中的结论得到AE＝AD＝5，BF＝BD＝7，AC＝5+r，BC＝7+r，再利用勾股定理得到（5+r）2+（7+r）2＝（5+7）2，求出r得到AC＝﹣1，BC＝+1，然后根据三角形面积公式求解；

（3）设⊙O的半径为r，与（2）一样得到AE＝AD＝m，BF＝BD＝n，AC＝m+r，BC＝n+r，利用勾股定理得到（m+r）2+（n+r）2＝（m+n）2，解得r＝ 或r＝（舍去），所以AC＝），BC＝，然后利用勾股定理计算三角形的面积即可．

解：（1）连接OD、OE、OF，如图，设⊙O的半径为r，

在Rt△ABC中，AB＝＝5，

∵Rt△ABC的内切圆⊙O，切点分别为点D、E、F，

∴OE⊥AC，OF⊥BC，CE＝CF，AE＝AD，BF＝BD，

易得四边形CFOE为正方形，

∴CE＝CF＝OE＝r，

∴AD＝AE＝3﹣r，BD＝BF＝4﹣r，

∴3﹣r+4﹣r＝5，解得r＝1，

即△ABC的内切圆半径为1；

（2）设⊙O的半径为r，

由（1）得AE＝AD＝5，BF＝BD＝7，

∴AC＝5+r，BC＝7+r，

在Rt△ABC中，（5+r）2+（7+r）2＝（5+7）2，解得r＝﹣6或r＝﹣6（舍去），

∴AC＝﹣6+5＝﹣1，BC＝﹣6+7＝+1，

∴S△ABC＝(﹣1)(+1）＝35；

（3）设⊙O的半径为r，

由（1）得AE＝AD＝m，BF＝BD＝n，

∴AC＝m+r，BC＝n+r，

在Rt△ABC中，（m+r）2+（n+r）2＝（m+n）2，解得r＝或r＝（舍去），

∴AC＝，BC＝，

∴S△ABC＝×AC×BC＝＝．

故答案为mn．