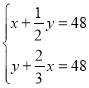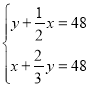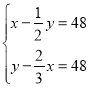题目内容
【题目】某校准备开春季运动会,学校要给学生买若干笔袋和笔记本作为奖品.购买2个笔袋和1个笔记本需花25元,购买3个笔袋和2个笔记本需花40元.
(1)求笔袋和笔记本的单价各是多少元?
(2)学校准备购买笔袋和笔记本共计180个,甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案,在甲商场累计购物超过1000元后,超出1000元的部分按90%收费,在乙商场累计购物超过500元后,超出500元的部分按95%收费,经过预算此次购物超过了1000元,求学校需要至少购买多少个笔袋,才能使到甲商场购物更省钱?
【答案】(1)笔袋单价为10元,笔记本单价为5元;(2)学校需要购买至少121个笔袋才能使到甲商场购买更省钱.
【解析】
(1)设笔袋单价为![]() 元,笔记本单价为
元,笔记本单价为![]() 元,根据“购买2个笔袋和1个笔记本需花25元,购买3个笔袋和2个笔记本需花40元”可列出二元一次方程组,解方程组即可得出答案.
元,根据“购买2个笔袋和1个笔记本需花25元,购买3个笔袋和2个笔记本需花40元”可列出二元一次方程组,解方程组即可得出答案.
(2)设学校需要购买![]() 个笔袋才能使到甲商场购买更省钱;则学校需要购买
个笔袋才能使到甲商场购买更省钱;则学校需要购买![]() 个笔记本,根据“在甲商场累计购物超过1000元后,超出1000元的部分按90%收费,在乙商场累计购物超过500元后,超出500元的部分按95%收费,经过预算此次购物超过了1000元”列出一元一次不等式,解之即可得出
个笔记本,根据“在甲商场累计购物超过1000元后,超出1000元的部分按90%收费,在乙商场累计购物超过500元后,超出500元的部分按95%收费,经过预算此次购物超过了1000元”列出一元一次不等式,解之即可得出![]() 的取值范围,进而得出
的取值范围,进而得出![]() 的最小整数值.
的最小整数值.
(1)解:设笔袋单价为![]() 元,笔记本单价为
元,笔记本单价为![]() 元。
元。
![]()
解得:![]()
答:笔袋单价为10元,笔记本单价为5元.
(2)设学校需要购买![]() 个笔袋才能使到甲商场购买更省钱;则学校需要购买
个笔袋才能使到甲商场购买更省钱;则学校需要购买![]() 个笔记本;
个笔记本;
学校购买两种物品共需花费![]() 元
元
∵经过预算此次购物超过了1000元
∵![]()
解得:![]()
根据题意可列式为:![]()
解得:![]()
∵![]() 为正整数
为正整数
∴![]() 最小值为121
最小值为121
答;学校需要购买至少121个笔袋才能使到甲商场购买更省钱.

 培优三好生系列答案
培优三好生系列答案【题目】2018年非洲猪瘟疫情暴发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价y1(元)与月份x(1≤x≤12,且x为整数)之间满足一次函数关系,如下表所示.每千克猪肉的成本y2(元)与月份x(1≤x≤12,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,如图所示.
月份x | … | 3 | 4 | 5 | 6 | … |
售价y1/元 | … | 12 | 14 | 16 | 18 | … |

(1)求y1与x之间的函数关系式.
(2)求y2与x之间的函数关系式.
(3)设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数关系式,哪个月份销售每千克猪肉所第获得的利润最大?最大利润是多少元?