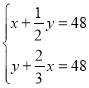题目内容
【题目】为节能减排,某公交公司计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车2辆,B型公交车3辆,共需650万元;若购买A型公交车3辆,B型公交车2辆,共需600万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该线路上A型和B型公交车每辆年均载客量分别为80万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于830万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
【答案】(1)A型每辆需100万元,B型每辆需150万元;(2)所以共有三种采购方案:方案一:采购![]() 型6台,采购
型6台,采购![]() 型4台,方案二:采购
型4台,方案二:采购![]() 型7台,采购
型7台,采购![]() 型3台,方案三:采购
型3台,方案三:采购![]() 型8台,采购
型8台,采购![]() 型2台;当采购
型2台;当采购![]() 型
型![]() 辆,采购
辆,采购![]() 型
型![]() 辆时,费用最低,最低费用为:1100万元.
辆时,费用最低,最低费用为:1100万元.
【解析】
(1)设A型需![]() 万元,B型需
万元,B型需![]() 万元,根据题意列出二元一次方程组即可求解;
万元,根据题意列出二元一次方程组即可求解;
(2)设购买![]() 型
型![]() 辆,购买
辆,购买![]() 型
型![]() 辆,根据题意列出不等式组即可求解.
辆,根据题意列出不等式组即可求解.
解(1)设A型需![]() 万元,B型需
万元,B型需![]() 万元,由题意得
万元,由题意得
![]()
解得![]()
∴A型每辆需100万元,B型每辆需150万元
(2)设购买![]() 型
型![]() 辆,购买
辆,购买![]() 型
型![]() 辆,得
辆,得
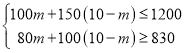
∴![]() ,
,
又![]() 为自然数,
为自然数,
∴![]() 或
或![]() 或
或![]() ,所以共有三种采购方案
,所以共有三种采购方案
方案一:采购![]() 型6台,采购
型6台,采购![]() 型4台
型4台
方案二:采购![]() 型7台,采购
型7台,采购![]() 型3台
型3台
方案三:采购![]() 型8台,采购
型8台,采购![]() 型2台
型2台
设总费用为![]() 元,则有
元,则有![]() ,即
,即
![]() 且
且![]() 为正整数)
为正整数)
∴![]() 随
随![]() 的增大而减小,当采购
的增大而减小,当采购![]() 型
型![]() 辆,采购
辆,采购![]() 型
型![]() 辆时,费用最低.
辆时,费用最低.
最低费用为:![]() 万元.
万元.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案【题目】2018年非洲猪瘟疫情暴发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价y1(元)与月份x(1≤x≤12,且x为整数)之间满足一次函数关系,如下表所示.每千克猪肉的成本y2(元)与月份x(1≤x≤12,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,如图所示.
月份x | … | 3 | 4 | 5 | 6 | … |
售价y1/元 | … | 12 | 14 | 16 | 18 | … |

(1)求y1与x之间的函数关系式.
(2)求y2与x之间的函数关系式.
(3)设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数关系式,哪个月份销售每千克猪肉所第获得的利润最大?最大利润是多少元?