Question

【题目】如图①，若抛物线的顶点在抛物线上，抛物线的顶点在抛物线上，（点与点不重合），我们把这样的两条抛物线和，互称为“友好”抛物线．

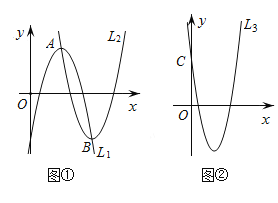
（1）一条抛物线的“友好”抛物线有 条；

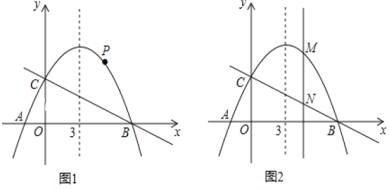
（2）如图②，已知抛物线与轴相交于点，点关于抛物线的对称轴的对称点为点，求以点为顶点的的“友好”抛物线的表达式；

（3）若抛物线的“友好”抛物线的解析式为，请直接写出与的关系式．

Answer 1

【答案】（1）无数；（2）；（3）

【解析】

(1)根据题目给的定义即可判断一条抛物线有无数条”友好”抛物线.

(2)先设出L4的解析式,求出L3的坐标轴和顶点坐标,再将顶点坐标代入L4的解析式中即可求解.

(3)根据两个抛物线的顶点都在对方抛物线上,列式求解即可.

（1）根据“友好”抛物线的定义,只需要确定原函数顶点和抛物线任意一点做“友好”抛物线的顶点即可作出“友好”抛物线,因此有无数条.

∴答案为:无数.

（2）把化为顶点式，得

顶点坐标为，

对称轴为

点坐标为，

点关于对称轴的对称点的坐标为，

设的解析式为，

把代入，得

.

解得.

的“友好”抛物线的表达式为：.

（3）由题意可得: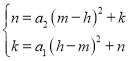,整理得,(a1+a2)(m-h)2=0,

∵顶点不重合,∴m≠h,

∴.