Question

【题目】如图，在△ABC中，AC＝12cm，BC＝16cm，AB＝20cm，∠CAB的角平分线AD交BC于点D．

（1）根据题意将图形补画完整（要求：尺规作图保留作图痕迹，不写作法）；

（2）求△ABD的面积．

Answer 1

【答案】（1）见解析（2）60

【解析】

（1）根据角平分线的基本作图作出角平分线即可；

（2）根据角平分线的性质，构造直角三角形，然后根据角平分线的性质和三角形的面积求解即可.

（1）如图所示：

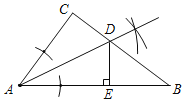
（2）如图，过点D作DE⊥AB于点E，

由角平分线的性质得CD=DE．

∵AC2+BC2=122+162=202=AB2，

∴△ABC是直角三角形，∠ACB=90°，

∵AD平分∠CAB，DE⊥AB，DC⊥AC，∴CD=DE，

∵S△ABC=S△ABD+S△ACD，∴BCAC=ABDE+ACCD，

∴10DE+6CD=96，即CD=DE=6，∴S△ABD=ABDE=60cm2．