题目内容
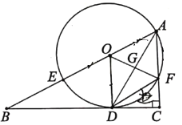
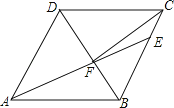
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是![]() ;③△ADF与△EBF的面积比为3:2,④△ABF的面积为
;③△ADF与△EBF的面积比为3:2,④△ABF的面积为![]() ,其中一定成立的有( )个.
,其中一定成立的有( )个.
A.2B.3C.1D.4
【答案】B
【解析】
根据菱形的性质得:△ABF和△CBF全等的条件,进而判断①的正误;过E作AB的垂线段,再解直角三角形求出垂线段的长度,进而判断②的正误;利用相似三角形的性质,求出面积比,便可判断③的正误;利用解直角三角形和等边三角形的性质,求出△ABC中,AB边上的高,进而求得面积,判断④的正误.
解:∵四边形ABCD是菱形,
∴AB=BC=6,
∵∠DAB=60°,
∴AB=AD=DB,∠ABD=∠DBC=60°,
在△ABF与△CBF中,
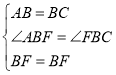 ,
,
∴△ABF≌△CBF(SAS),故①正确;
如图:过点E作EG⊥AB,过点F作MH⊥CD,MH⊥AB,
∵CE=2,BC=6,∠ABC=120°,
∴BE=6﹣2=4,
∵EG⊥AB,
∴EG=2![]() ,故②正确;
,故②正确;
∵AD∥BE,
∴△ADF∽△EBF,
∴![]() ,故③错误;
,故③错误;
∵△ADF∽△EBF,
∴![]() ,
,
∵BD=6,
∴BF![]() ,
,
∴FH=BFsin∠FBH![]() ,
,
∴![]() ,故④正确;
,故④正确;
故选:B.

练习册系列答案
相关题目