题目内容
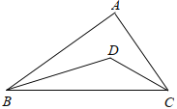
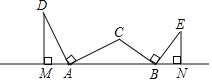
【题目】如图,在△ABC中,∠ACB为钝角,把边AC绕点A沿逆时针方向旋转90°得AD,把边BC绕点B沿顺时针方向旋转90°得BE,作DM⊥AB于点M,EN⊥AB于点N,若AB=5,EN=2,则DM=_____.
【答案】3
【解析】
过点C作CF⊥AB于点F,由旋转的性质可得AD=AC,BE=BC,利用“一线三等角“证得∠D=∠CAF,从而可判定△DAM≌△ACF(AAS),则DM=AF.同理可证,△BFC≌△ENB(AAS),则BF=EN=2,再由AB=5,可得AF,即DM的值.
解:过点C作CF⊥AB于点F,如图所示:

∵旋转,
∴AD=AC,BE=BC,
∵DM⊥AB于点M,EN⊥AB于点N,CF⊥AB于点F,
∴∠AMD=∠AFC=∠BFC=∠BNE=90°,
∴∠D+∠DAM=90°,
∵∠CAD=90°,
∴∠CAF+∠DAM=90°,
∴∠D=∠CAF,
∴在△DAM和△ACF中,
∴△DAM≌△ACF(AAS),
∴DM=AF.
同理可证,△BFC≌△ENB(AAS),
∴BF=EN=2,
∵AB=5,
∴AF=3,
∴DM=3.
故答案为:3.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目