题目内容
【题目】如图1,△ABC内接于![]() ,点D是
,点D是![]() 的中点,且与点C位于AB的异侧,CD交AB于点E.
的中点,且与点C位于AB的异侧,CD交AB于点E.
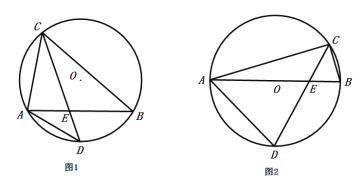
(1)求证:△ADE∽△CDA
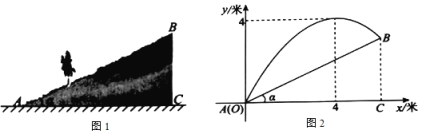
(2)如图2,若![]() 的直径AB
的直径AB![]() ,CE=2,求AD和CD的长.
,CE=2,求AD和CD的长.
【答案】(1)详见解析;(2)![]() ,
,![]() .
.
【解析】
(1)根据“同弧或等弧所对的圆周角相等”证角相等,进而可证三角形相似;
(2)连接BD,先证三角形ADB为等腰直角三角形,求出AD的长,再根据(1)中的相似三角形得出比例式求解即可.
(1)∵点D是![]() 的中点,
的中点,
∴![]()
∴∠ACD=∠BAD
∵∠ADE=∠CDA
∴△ADE∽△CDA
(2)连结BD,
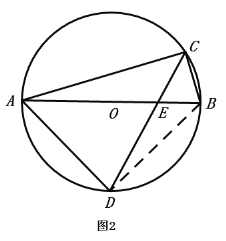
∵点D时![]() 的中点,
的中点,
∴AD=BD
∵AB是![]() 的直径,
的直径,
∴∠ADB=90°
∴△ADB为等腰直角三角形,
∴![]() ,
,
由(1)得△ADE∽△CDA
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得CD=8或-6(负值舍去)
∴CD=8.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目