Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°ŅŃ‚–őABCD‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–ĶńőĽ÷√»ÁÕľňý ĺ£¨∂‘Ĺ«ŌŖAC”ŽBDĶńĹĽĶ„E«°ļ√‘ŕy÷Š…Ō£¨ĻżĶ„DļÕBCĶń÷–Ķ„HĶń÷ĪŌŖĹĽAC”ŕĶ„F£¨ŌŖ∂őDE£¨CDĶń≥§ «∑Ĺ≥Őx2©Ā9x+18=0ĶńŃĹłý£¨«ŽĹ‚īūŌ¬Ń–ő Ő‚£ļ
£®1£©«ůĶ„DĶń◊ÝĪÍ£Ľ
£®2£©»Ű∑īĪ»ņżļĮ ży=![]() £®k°Ŕ0£©ĶńÕľŌůĺ≠ĻżĶ„H£¨‘Úk=°° °°£Ľ
£®k°Ŕ0£©ĶńÕľŌůĺ≠ĻżĶ„H£¨‘Úk=°° °°£Ľ
£®3£©Ķ„Q‘ŕ÷ĪŌŖBD…Ō£¨‘ŕ÷ĪŌŖDH…Ō «∑Ůīś‘ŕĶ„P£¨ Ļ“‘Ķ„F£¨C£¨P£¨Qő™∂•Ķ„ĶńňńĪŖ–ő «∆Ĺ––ňńĪŖ–ő£Ņ»Űīś‘ŕ£¨«Ž÷ĪĹ”–ī≥ŲĶ„PĶń◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ

°ĺīūįł°Ņ£®1£©£®©Ā![]() £¨3
£¨3![]() £©£®2£©
£©£®2£©![]() £®3£©£®
£®3£©£®![]() £¨
£¨![]() £©ĽÚ£®©Ā
£©ĽÚ£®©Ā![]() £¨5
£¨5![]() £©ĽÚ£®
£©ĽÚ£®![]() £¨©Ā
£¨©Ā![]() £©
£©
°ĺĹ‚őŲ°Ņ
£®1£©”…ŌŖ∂őDE£¨CDĶń≥§ «∑Ĺ≥Őx2©Ā9x+18=0ĶńŃĹłý£¨«“CD£ĺDE£¨Ņ…«ů≥ŲCD°ĘDEĶń≥§£¨”…ňńĪŖ–őABCD «Ń‚–ő£¨ņŻ”√Ń‚–őĶń–‘÷ Ņ…«ůĶ√DĶ„Ķń◊ÝĪÍ.
(2)”…£®1£©Ņ…Ķ√OB°ĘCM£¨Ņ…Ķ√B°ĘC◊ÝĪÍ£¨ĹÝ∂Ý«ůĶ√HĶ„◊ÝĪÍ£¨”…∑īĪ»ņżļĮ ży=![]() £®k°Ŕ0£©ĶńÕľŌůĺ≠ĻżĶ„H£¨Ņ…«ůĶńkĶń÷Ķ;
£®k°Ŕ0£©ĶńÕľŌůĺ≠ĻżĶ„H£¨Ņ…«ůĶńkĶń÷Ķ;
(3)∑÷Īū“‘CFő™∆Ĺ––ňńĪŖ–őĶń“ĽĪŖĽÚ’Ŗő™∂‘Ĺ«ŌŖĶń«ť–őĹÝ––Ő÷¬ŘľīŅ….
£®1£©x2©Ā9x+18=0£¨
£®x©Ā3£©£®x©Ā6£©=0£¨
x=3ĽÚ6£¨
°ŖCD£ĺDE£¨
°ŗCD=6£¨DE=3£¨
°ŖňńĪŖ–őABCD «Ń‚–ő£¨
°ŗAC°ÕBD£¨AE=EC=![]() =3
=3![]() £¨
£¨
°ŗ°ŌDCA=30°„£¨°ŌEDC=60°„£¨
Rt°ųDEM÷–£¨°ŌDEM=30°„£¨
°ŗDM=![]() DE=
DE=![]() £¨
£¨
°ŖOM°ÕAB£¨
°ŗSŃ‚–őABCD=![]() ACBD=CDOM£¨
ACBD=CDOM£¨
°ŗ![]() =6OM£¨OM=3
=6OM£¨OM=3![]() £¨
£¨
°ŗD£®©Ā![]() £¨3
£¨3![]() £©£Ľ
£©£Ľ
£®2£©°ŖOB=DM=![]() £¨CM=6©Ā
£¨CM=6©Ā![]() =
=![]() £¨
£¨
°ŗB£®![]() £¨0£©£¨C£®
£¨0£©£¨C£®![]() £¨3
£¨3![]() £©£¨
£©£¨
°ŖH «BCĶń÷–Ķ„£¨
°ŗH£®3£¨![]() £©£¨
£©£¨
°ŗk=3°Ń![]() =
=![]() £Ľ
£Ľ
Ļ īūįłő™£ļ![]() £Ľ
£Ľ
£®3£©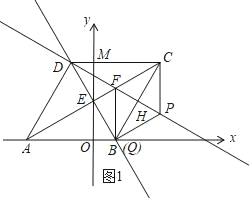
ĘŔ°ŖDC=BC£¨°ŌDCB=60°„£¨
°ŗ°ųDCB «Ķ»ĪŖ»żĹ«–ő£¨
°ŖH «BCĶń÷–Ķ„£¨
°ŗDH°ÕBC£¨
°ŗĶĪQ”ŽB÷ōļŌ Ī£¨»ÁÕľ1£¨ňńĪŖ–őCFQP «∆Ĺ––ňńĪŖ–ő£¨
°ŖFC=FB£¨
°ŗ°ŌFCB=°ŌFBC=30°„£¨
°ŗ°ŌABF=°ŌABC©Ā°ŌCBF=120°„©Ā30°„=90°„£¨
°ŗAB°ÕBF£¨CP°ÕAB£¨
Rt°ųABF÷–£¨°ŌFAB=30°„£¨AB=6£¨
°ŗFB=2![]() =CP£¨
=CP£¨
°ŗP£®![]() £¨
£¨![]() £©£Ľ
£©£Ľ
Ęŕ
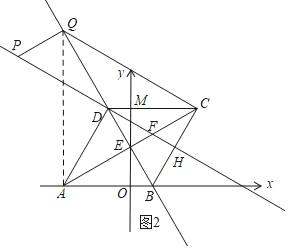
»ÁÕľ2£¨°ŖňńĪŖ–őQPFC «∆Ĺ––ňńĪŖ–ő£¨
°ŗCQ°őPH£¨
”…ĘŔ÷™£ļPH°ÕBC£¨
°ŗCQ°ÕBC£¨
Rt°ųQBC÷–£¨BC=6£¨°ŌQBC=60°„£¨
°ŗ°ŌBQC=30°„£¨
°ŗCQ=6![]() £¨
£¨
ѨŔQA£¨
°ŖAE=EC£¨QE°ÕAC£¨
°ŗQA=QC=6![]() £¨
£¨
°ŗ°ŌQAC=°ŌQCA=60°„£¨°ŌCAB=30°„£¨
°ŗ°ŌQAB=90°„£¨
°ŗQ£®©Ā![]() £¨6
£¨6![]() £©£¨
£©£¨
”…ĘŔ÷™£ļF£®![]() £¨2
£¨2![]() £©£¨
£©£¨
”…FĶĹCĶń∆Ĺ“∆Ļś¬…Ņ…Ķ√PĶĹQĶń∆Ĺ“∆Ļś¬…£¨‘ÚP£®©Ā![]() ©Ā3£¨6
©Ā3£¨6![]() ©Ā
©Ā![]() £©£¨ľīP£®©Ā
£©£¨ľīP£®©Ā![]() £¨5
£¨5![]() £©£Ľ
£©£Ľ
ĘŘ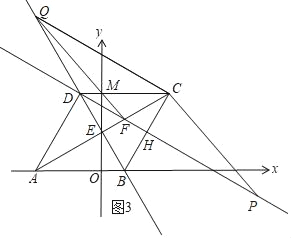
»ÁÕľ3£¨ňńĪŖ–őCQFP «∆Ĺ––ňńĪŖ–ő£¨
Õ¨ņŪ÷™£ļQ£®©Ā![]() £¨6
£¨6![]() £©£¨F£®
£©£¨F£®![]() £¨2
£¨2![]() £©£¨C£®
£©£¨C£®![]() £¨3
£¨3![]() £©£¨
£©£¨
°ŗP£®![]() £¨©Ā
£¨©Ā![]() £©£Ľ
£©£Ľ
◊Ř…Ōňý Ų£¨Ķ„PĶń◊ÝĪÍő™£ļ£®![]() £¨
£¨![]() £©ĽÚ£®©Ā
£©ĽÚ£®©Ā![]() £¨5
£¨5![]() £©ĽÚ£®
£©ĽÚ£®![]() £¨©Ā
£¨©Ā![]() £©£ģ
£©£ģ

°ĺŐ‚ńŅ°Ņń≥∑Áĺį«Ýľ∆Ľģ‘ŕ¬ŐĽĮ«Ý”Ú÷÷÷≤“Ý–” ų£¨Ō÷ľ◊°Ę““ŃĹľ“”–ŌŗÕ¨Ķń“Ý–” ų√ÁŅ…Ļ©—°‘Ů£¨∆šĺŖŐŚŌķ Ř∑Ĺįł»ÁŌ¬£ļ
ľ◊ | ““ | ||
Ļļ ų√Á żŃŅ | Ōķ ŘĶ•ľŘ | Ļļ ų√Á żŃŅ | Ōķ ŘĶ•ľŘ |
≤Ľ≥¨Ļż500Ņ√ Ī | 800‘™/Ņ√ | ≤Ľ≥¨Ļż1000Ņ√ Ī | 800‘™/Ņ√ |
≥¨Ļż500Ņ√Ķń≤Ņ∑÷ | 700‘™/Ņ√ | ≥¨Ļż1000Ņ√Ķń≤Ņ∑÷ | 600‘™/Ņ√ |
…ŤĻļ¬Ú“Ý–” ų√ÁxŅ√£¨ĶĹŃĹľ“Ļļ¬Úňý–Ť∑—”√∑÷Īūő™yľ◊‘™°Ęy““‘™
(1)ł√∑Áĺį«Ý–Ť“™Ļļ¬Ú800Ņ√“Ý–” ų√Á£¨»Ű∂ľ‘ŕľ◊ľ“Ļļ¬Úňý“™∑—”√ő™°° °°‘™£¨»Ű∂ľ‘ŕ““ľ“Ļļ¬Úňý–Ť∑—”√ő™°° °°‘™£Ľ
(2)ĶĪx£ĺ1000 Ī£¨∑÷Īū«ů≥Ųyľ◊°Ęy““”Žx÷ģľšĶńļĮ żĻōŌĶ Ĺ£Ľ
(3)»ÁĻŻń„ «ł√∑Áĺį«ÝĶńłļ‘ū»ň£¨Ļļ¬Ú ų√Á Ī”– ≤√ī∑Ĺįł£¨ő™ ≤√ī£Ņ





