题目内容
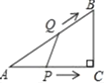
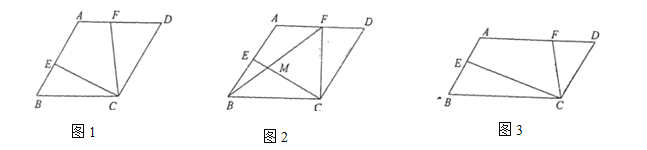
【题目】如图，菱形
的边长为
，点
是对角线
的中点．点
是
边上一动点，
延长线交
于点
则
长度可能为（ ）
A.
B.
C.
D.
【答案】B
【解析】
当GH⊥AB时，GH的长度最短；当GH与AC重合时，GH的长度最长，故可得出GH的取值范围，从而判定选项．
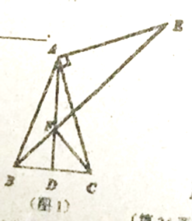
如下图，当GH⊥AB时，GH的长度最短，过点C作AB的垂线交AB延长线于点F
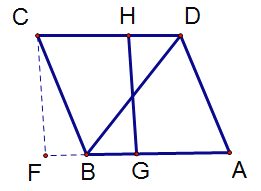
∵四边形ABCD是菱形，
∴FG∥CH
∵GH⊥AB，CF⊥AB,
HG
CF
∴四边形GHCF是矩形
∵菱形ABCD中，∠A=60°，边长为2
∴CB=2，∠CBF=60°
∴在Rt △CBF中，FB=1，CF=
∴HG=
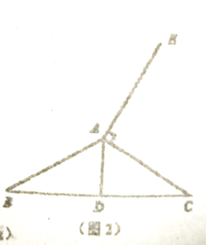
如下图，当GH与AC重合时，GH的长度最长，过点C作AB的垂线交AB延长线于点F
∵∠BAD=60°，菱形ABCD的边长为2
∴∠BAC=∠BCA=30°，CB=2
∴∠CBF=60°
∴在Rt△CBF中，BF=1
∴FA=3
∴在Rt△CAF中，CF=，AC=2
∴≤GH≤2
故选：B
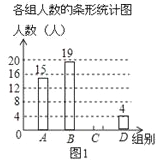
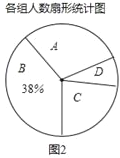
阅读快车系列答案
【题目】为庆祝建国70周年，某校举办了爱我中华知识竞赛活动．该校南、北两个校区七年级各有300名学生参加竞赛活动．为了解这两个校区参赛学生成绩情况，从中各随机抽取了10名学生的成绩进行调查，过程如下：
（收集、整理、描述数据）根据随机抽取的10名学生的成绩，制作了如下统计图表：
（说明：成绩90分及以上为优秀，80-89分为良好，60-79分为合格，60分以下为不合格）
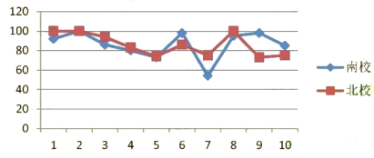
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
南校 | 92 | 100 | 86 | 80 | 73 | 98 | 54 | 95 | 98 | 85 |
北校 | 100 | 100 | 94 | 83 | 74 | 86 | 75 | 100 | 73 | 75 |
（分析数据）对上述数据进行分析，分别求出了两组样本数据的平均数、中位数、众数如下表：
校区 | 平均数（分） | 中位数（分） | 众数（分） |
南校 | 87 | 90．5 | |
北校 | 86 | 100 |
（得出结论）综合上述统计全过程，回答下列问题：
（1）补全表格．
（2）估计北校七年级学生竞赛成绩为优秀的人数．
（3）你认为哪个校区的七年级学生竞赛成绩比较好？说明你的理由．（从两个不同的角度说明推断的合理性）
