题目内容
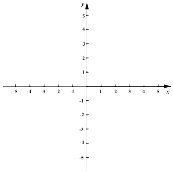
【题目】在平面直角坐标系
中，抛物线
与直线
交于点
，且点的横坐标为
．
（1）请用
的代数式表示
；
（2）点
在直线
上，点的横坐标为
，点
的坐标为
．
①若抛物线
过点，求该抛物线的解析式；
②若抛物线与线段
恰有一个交点，直接写出的取值范围．
【答案】（1）
（2）
（3）
或
【解析】
（1）把x=-2代入直线l的解析式求得
，再把代入抛物线的解析式即可得；
（2）①把x=-1代入直线l的解析式求得
，再根据待定系数法求出抛物线解析式即可；②先根据题意求得
或，再分情况：1）当抛物线顶点在线段BC上时，2）当抛物线与线段BC有一个交点时，分别求解即可．
（1）把x=-2代入直线l的解析式得
∴
把代入抛物线的解析式得
解得；
（2）①把x=-1代入直线l的解析式得
∴
把代入抛物线的解析式得
解得
∴
∴；
②∵
∴对称轴x=b开口向下，顶点为
当抛物线M与线段BC恰有一个交点时，交点纵坐标为5，此时
整理得
∵
∴
解得或
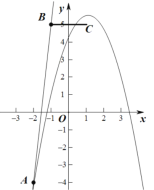
当抛物线顶点在线段BC上时，如图
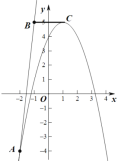或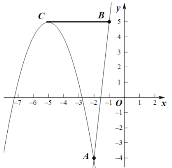
当
时，抛物线与线段BC恰有一个交点
解得b=1或b=-5，此时顶点为
或
当抛物线与线段BC有一个交点时，如图
或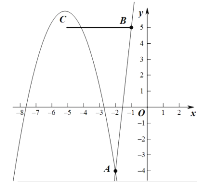
如上左图中，此时交点为
应在点右侧即
解得，
或
（舍去）与最初取值矛盾
如上右图中，此时交点为
，应在点
的右侧即
解得或
故抛物线与线段BC恰有一个交点时，或．
练习册系列答案
相关题目
