题目内容
【题目】图1是一个倾斜角为
的斜坡的横截面，
．斜坡顶端B与地面的距离
为3米．为了对这个斜坡上的绿地进行喷灌，在斜坡底端安装了一个喷头A，喷头A喷出的水珠在空中走过的曲线可以看作抛物线的一部分．设喷出水珠的竖直高度为y（单位：米）（水珠的竖直高度是指水珠与地面的距离），水珠与喷头A的水平距离为x（单位：米），y与x之间近似满足函数关系
（a，b是常数，
），图2记录了x与y的相关数据．
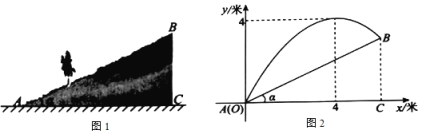
（1）求y关于x的函数关系式；
（2）斜坡上有一棵高1.8米的树，它与喷头A的水平距离为2米，通过计算判断从A喷出的水珠能否越过这棵树．
【答案】（1）
，（2）从A喷出的水珠能越过这棵树．
【解析】
(1)根据待定系数法，即可求得二次函数的解析式，
(2)先求出树顶离底面的高度，再求出当x=2时，二次函数的值，进行二者的大小关系，即可得到答案.
（1）∵
，BC=3，
∴AC=6，即：点B坐标是：（6，3），
把（4，4）（6，3）代入：
，
得：
，解得：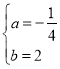
，
∴二次函数的解析式是：
（2）树顶离底面高度为：1.8+2×
=1.8+2×
=2.8，
当x=2，代入，得：
=3>2.8，
∴从A喷出的水珠能越过这棵树．
练习册系列答案
相关题目
