题目内容
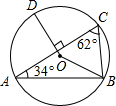
如图，已知⊙O中，OA=2，AC是⊙O的直径，AC⊥BD于E，∠A=30°．
（1）求BD的长；
（2）求圆中阴影部分的面积．
（3）若用阴影部分扇形OBD围成一个圆锥的侧面，请求出这个圆锥的底面圆的半径．
（1）求BD的长；
（2）求圆中阴影部分的面积．
（3）若用阴影部分扇形OBD围成一个圆锥的侧面，请求出这个圆锥的底面圆的半径．
（1）∵AC是⊙O的直径，AC⊥BD于E，
∴BD=2BE，
∵∠A=30°，
∴∠ABD=60°，
∵OA=OB=2，
∴∠ABO=∠A=30°，∠OBE=30°，
∴BE=OB•cos30°=2×
=
，
∴BD=2BE=2
；
（2）∵∠A=30°，
∴∠BOC=60°
∵AC⊥BD，
∴
=
，
∴∠BOD=2∠BOC=120°，
∴S阴影=
=
；
（3）设这个圆锥的底面圆的半径为r，则2πr=
，解得r=
．
答：这个圆锥的底面圆的半径为
．
∴BD=2BE，
∵∠A=30°，
∴∠ABD=60°，
∵OA=OB=2，
∴∠ABO=∠A=30°，∠OBE=30°，
∴BE=OB•cos30°=2×
| ||
| 2 |
| 3 |
∴BD=2BE=2
| 3 |
（2）∵∠A=30°，
∴∠BOC=60°
∵AC⊥BD，
∴
 |
| BC |
|
| CD |
∴∠BOD=2∠BOC=120°，
∴S阴影=
| 120π×52 |
| 360 |
| 25π |
| 3 |
（3）设这个圆锥的底面圆的半径为r，则2πr=
| 120×π×5 |
| 180 |
| 5 |
| 3 |
答：这个圆锥的底面圆的半径为
| 5 |
| 3 |
练习册系列答案
中考解读考点精练系列答案
相关题目
