题目内容
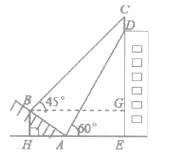
【题目】某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60度,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45度,已知山坡AB的坡度i=1: ![]() ,AB=10米,AE=15米.
,AB=10米,AE=15米.
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.(保留根号)
【答案】
(1)
解:Rt△ABH中,i=tan∠BAH= ![]() =
= ![]() ,
,
∴∠BAH=30°,
∴BH= ![]() AB=5(米).
AB=5(米).
(2)
解:过B作BG⊥DE于G,
由(1)得:BH=5,AH=ABcos∠BAH=10× ![]() =5
=5 ![]() ,
,
∴BG=AH+AE=5 ![]() +15,
+15,
Rt△BGC中,∠CBG=45°,
∴CG=BG=5 ![]() +15,
+15,
∴Rt△ADE中,∠DAE=60°,AE=15,
∴DE= ![]() AE=15
AE=15 ![]() .
.
∴CD=CG+GE-DE=5 ![]() +15+5-15
+15+5-15 ![]() =20-10
=20-10 ![]() (米).
(米).
答案:宣传牌CD高约(20-10 ![]() )米.
)米.
【解析】(1)坡比i= ![]() =tan∠BAH,又因为BH⊥AH,则可得∠BAH,由AB可解出BH;(2)由(1)得:BH=5,AH=ABcos∠BAH求出AH,则BG=AH+AE;Rt△BGC中,∠CBG=45°,则CG=BG,Rt△ADE中,∠DAE=60°,DE=
=tan∠BAH,又因为BH⊥AH,则可得∠BAH,由AB可解出BH;(2)由(1)得:BH=5,AH=ABcos∠BAH求出AH,则BG=AH+AE;Rt△BGC中,∠CBG=45°,则CG=BG,Rt△ADE中,∠DAE=60°,DE= ![]() AE,则CD=CG+GE-DE.
AE,则CD=CG+GE-DE.
【考点精析】掌握关于坡度坡角问题是解答本题的根本,需要知道坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目