题目内容
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
(1)已知BD= ![]() ,求正方形ABCD的边长;
,求正方形ABCD的边长;
(2)猜想线段CM与CN的数量关系并加以证明.
【答案】
(1)
解:∵四边形 ABCD 是正方形,
∴△ABD 是等腰直角三角形,
∴2AB2=BD2,
∵BD= ![]() ,∴AB=1,
,∴AB=1,
∴正方形ABCD的边长为1.
(2)
解:CN= ![]() CM.
CM.
证明如下:∵CF=CA,CE是∠ACF的平分线,
∴CE⊥AF,∴∠AEN=∠CBN=90°, 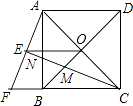
∵∠ANE=∠CNB,∴∠BAF=∠BCN,
在△ABF 和△CBN 中,
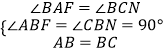
∴△ABF≌△CBN(ASA),∴AF=CN,
∵∠BAF=∠BCN,∠ACN=∠BCN,∴∠BAF=∠OCM,
∵四边形ABCD是正方形,∴AC⊥BD,∴∠ABF=∠COM=90°,
∴△ABF~△COM,
∴ ![]() ,∴
,∴ ![]() ,
,
即CN= ![]() CM.
CM.
【解析】(1)由正方形的性质易得2AB2=BD2 , 而BD已知,即可解出AB;(2)根据“ASA”,证明△ABF≌△CBN,则AF=CN;再证明△ABF~△COM,则 ![]() ,即
,即 ![]() .
.

【题目】如图,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边的活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡,改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如下表:
x(cm) | 10 | 15 | 20 | 25 | 30 |
y(g) | 30 | 20 | 15 | 12 | 10 |

(1)把上表中(x,y)的各组对应值作为点的坐标,在坐标系中描出相应的点,用平滑曲线连接这些点;
(2)观察所画的图象,猜测y与x之间的函数关系,求出函数关系式并加以验证;
(3)当砝码的质量为24g时,活动托盘B与点O的距离是多少cm?
(4)当活动托盘B往左移动时,应往活动托盘B中添加还是减少砝码?
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | 1 | 2 | 3 | 4 | 5 | … |
y | … | 0 | ﹣3 | ﹣6 | ﹣6 | ﹣3 | … |
从上表可知,下列说法中正确的有( )
① ![]() =6;②函数y=ax2+bx+c的最小值为﹣6;③抛物线的对称轴是x=
=6;②函数y=ax2+bx+c的最小值为﹣6;③抛物线的对称轴是x= ![]() ;④方程ax2+bx+c=0有两个正整数解.
;④方程ax2+bx+c=0有两个正整数解.
A.1个
B.2个
C.3个
D.4个