题目内容
【题目】如图,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点,BP的延长线交⊙O于Q,过Q的⊙O的切线交OA的延长线于R.求证:RP=RQ. 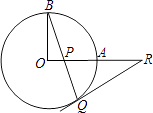
【答案】证明:连接OQ, 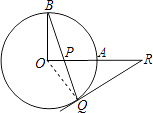
∵RQ是⊙O的切线,
∴OQ⊥QR,
∴∠OQB+∠BQR=90°.
∵OA⊥OB,
∴∠OPB+∠B=90°.
又∵OB=OQ,
∴∠OQB=∠B.
∴∠PQR=∠BPO=∠RPQ.
∴RP=RQ.
【解析】首先连接OQ,由切线的性质,可得∴∠OQB+∠BQR=90°,又由OA⊥OB,可得∠OPB+∠B=90°,继而可证得∠PQR=∠BPO=∠RPQ,则可证得RP=RQ.
【考点精析】利用切线的性质定理对题目进行判断即可得到答案,需要熟知切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

练习册系列答案
相关题目