题目内容
【题目】如图,在菱形ABCD和菱形BEFG中,点A、B、E在同一直线上,P是线段DF的中点,连接PG,PC.若∠ABC=∠BEF=60°,则 ![]() =( )
=( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:如图,延长GP交DC于点H,

∵P是线段DF的中点,
∴FP=DP,
由题意可知DC∥GF,
∴∠GFP=∠HDP,
∵∠GPF=∠HPD,
∴△GFP≌△HDP,
∴GP=HP,GF=HD,
∵四边形ABCD是菱形,
∴CD=CB,
∴CG=CH,
∴△CHG是等腰三角形,
∴PG⊥PC,(三线合一)
又∵∠ABC=∠BEF=60°,
∴∠GCP=60°,
∴ ![]() =
= ![]() ;
;
所以答案是:B.
【考点精析】掌握菱形的性质和锐角三角函数的定义是解答本题的根本,需要知道菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
【题目】在学校组积的科学家素养竞赛中,每班参加比赛的人数相同,成绩分为A、B、C、D四个等级,其中相应等级的得分依次记为90分、80分、70 分、60 分,学校将八年级(1)班和(2) 班的成绩整理并绘制成如下的统计图:
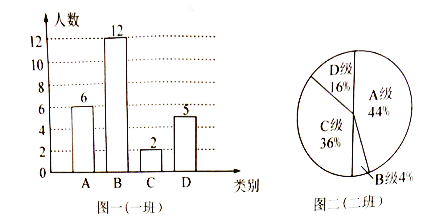
请你根据以上提供的信息解答下列问题:
(1) 此次竞赛中二 班成绩在70分以上(包括70分) 的人数有多少人?
(2) 补全下表中空缺的三个统计量:
平均数/ 分 | 中位数/ 分 | 众数/ 分 | |
一班 | 77.6 | 80 | _____________ |
二班 | _____________ | ______________ | 90 |
(3) 请根据上述图表对这次竞赛成绩进行分析,写出两个结论.