题目内容
【题目】如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E,若AB=8,AD=3,则△EB′C的周长为 . 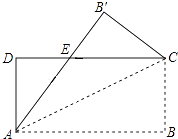
【答案】11
【解析】解:∵四边形ABCD为矩形,
∴B′C=BC=AD,∠B′=∠B=∠D=90°
∵∠B′EC=∠DEA,
在△AED和△CEB′中, 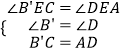 ,
,
∴△AED≌△CEB′(AAS),
∴DE=B′E,
∴△EB′C的周长=CE+B′E+B′C=CE+DE+AD=11,
所以答案是:11.
【考点精析】根据题目的已知条件,利用矩形的性质和翻折变换(折叠问题)的相关知识可以得到问题的答案,需要掌握矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

练习册系列答案
相关题目