题目内容
【题目】在平面直角坐标系中,点A、B的坐标分别为( 2,0 ),(4,0),点C的坐标为(m, ![]() m)(m为非负数),则CA+CB的最小值是_____.
m)(m为非负数),则CA+CB的最小值是_____.
【答案】2![]()
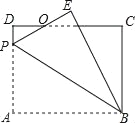
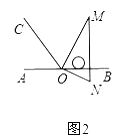
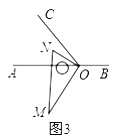
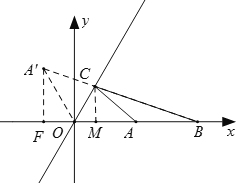
【解析】如图,作点A关于直线OC的对称点A′,连接A′B,则A′B的值就是CA+CB的最小值,
过点A′作A′F⊥x轴,垂足为F,过点C作CM⊥x轴,垂足为M,
∵点C的坐标为(m, ![]() m)(m为非负数),.
m)(m为非负数),.
∴OM=m,CM=![]() m,
m,
∵∠CMO=90°,∴tan∠COM=![]() =
=![]() ,∴∠COM=60°,
,∴∠COM=60°,
∵点A关于直线OC的对称点A′,
∴∠A′OC=∠COM=60°,
∴∠A′OF=60°,
∵OA′=OA=2,
∴OF=1,A′F=![]() ,
,
∵OB=4,BF=OB+OF,∴BF=5,
∴A′B=![]() ,
,
即AC+BC的最小值为2![]() ,
,
故答案为:2![]() .
.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目