Question

【题目】如图，Rt△ABC中，∠C=90°，∠A=30°，BC=1，D为AB中点，E为AC上一动点，BF∥AC交ED延长线于点F，则四边形BCEF周长的最小值为（　　）

A. 1+ B. 4 C. 2+ D. 2+

Answer 1

【答案】C

【解析】

由△ADE≌△BDF，推出BF=AE，推出四边形BCEF的周长=BC+CE+EF+BF=BC+AC+EF，由题意易知BC=1，AC=，即可推出EF最小时，四边形BCEF的周长最小，当DE⊥AC时，EF的值最小．

∵BF∥AC，

∴∠A=∠FBD，

在△ADE和△BDF中，

，

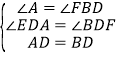∴△ADE≌△BDF，

∴BF=AE，

∴四边形BCEF的周长=BC+CE+EF+BF=BC+AC+EF，

由题意易知BC=1,AC=，

∴EF最小时，四边形BCEF的周长最小，当DE⊥AC时，EF的值最小，

∵BD=AD,DE∥CB，

∴CE=AE，

∴DE=BC=，

∴EF=2DE=1，

∴四边形BCEF周长的最小值为2+.

故答案选C.