题目内容
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+c与y轴交于点C,其顶点记为M,自变量x=﹣1和x=5对应的函数值相等.若点M在直线l:y=﹣12x+16上,点(3,﹣4)在抛物线上.
(1)求该抛物线的解析式;
(2)设y=ax2+bx+c对称轴右侧x轴上方的图象上任一点为P,在x轴上有一点A(﹣ ![]() ,0),试比较锐角∠PCO与∠ACO的大小(不必证明),并写出相应的P点横坐标x的取值范围.
,0),试比较锐角∠PCO与∠ACO的大小(不必证明),并写出相应的P点横坐标x的取值范围.
(3)直线l与抛物线另一交点记为B,Q为线段BM上一动点(点Q不与M重合),设Q点坐标为(t,n),过Q作QH⊥x轴于点H,将以点Q,H,O,C为顶点的四边形的面积S表示为t的函数,标出自变量t的取值范围,并求出S可能取得的最大值.
【答案】
(1)
解:∵自变量x=﹣1和x=5对应的函数值相等,
∴抛物线的对称轴为x=2.
∵点M在直线l:y=﹣12x+16上,
∴yM=﹣8.
设抛物线的解析式为y=a(x﹣2)2﹣8.
将(3,﹣4)代入得:a﹣8=﹣4,解得:a=4.
∴抛物线的解析式为y=4(x﹣2)2﹣8,整理得:y=4x2﹣16x+8
(2)
解:由题意得:C(0,8),M(2,﹣8),
如图,当∠PCO=∠ACO时,过P作PH⊥y轴于H,
设CP的延长线交x轴于D,
则△ACD是等腰三角形,
∴OD=OA= ![]() ,
,
∵P点的横坐标是x,
∴P点的纵坐标为4x2﹣16x+8,
∵PH∥OD,
∴△CHP∽△COD,
∴ ![]() ,
,
∴x= ![]() ,
,
过C作CE∥x轴交抛物线与E,
则CE=4,
设抛物线与x轴交于F,B,
则B(2+ ![]() ,0),
,0),
∴y=ax2+bx+c对称轴右侧x轴上方的图象上任一点为P,
∴当x= ![]() 时,∠PCO=∠ACO,
时,∠PCO=∠ACO,
当2+ ![]() <x<
<x< ![]() 时,∠PCO<∠ACO,
时,∠PCO<∠ACO,
当 ![]() <x<4时,∠PCO>∠ACO
<x<4时,∠PCO>∠ACO
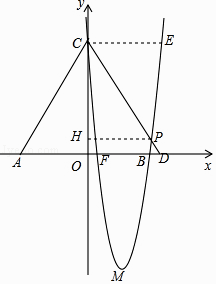
(3)
解:解方程组 ![]() ,
,
解得: ![]() ,
,
∴D(﹣1,28),
∵Q为线段BM上一动点(点Q不与M重合),
∴Q(t,﹣12t+16)(﹣1≤t<2),
①当﹣1≤t<0时,S= ![]() (﹣t)(﹣12t+16﹣8)+8(﹣t)=6t2﹣12t=6(t﹣1)2﹣6,
(﹣t)(﹣12t+16﹣8)+8(﹣t)=6t2﹣12t=6(t﹣1)2﹣6,
∵﹣1≤t<0,
∴当t=﹣1时,S最大=18;
②当0<t< ![]() 时,S=
时,S= ![]() t8+
t8+ ![]() t(﹣12t+16)=﹣6t2+12t=﹣6(t﹣1)2+6,∵0<t<
t(﹣12t+16)=﹣6t2+12t=﹣6(t﹣1)2+6,∵0<t< ![]() ,
,
∴当t=﹣1时,S最大=6;
③当 ![]() <t<2时,S=
<t<2时,S= ![]() t8+
t8+ ![]() (12t﹣16)=6t2﹣4t=6(t﹣
(12t﹣16)=6t2﹣4t=6(t﹣ ![]() )2﹣
)2﹣ ![]() ,
,
∵ ![]() <t<2,
<t<2,
∴此时S为最大值.
【解析】(1)根据已知条件得到抛物线的对称轴为x=2.设抛物线的解析式为y=a(x﹣2)2﹣8.将(3,﹣4)代入得抛物线的解析式为y=4(x﹣2)2﹣8,即可得到结论;(2)由题意得:C(0,8),M(2,﹣8),如图,当∠PCO=∠ACO时,过P作PH⊥y轴于H,设CP的延长线交x轴于D,则△ACD是等腰三角形,于是得到OD=OA= ![]() ,根据相似三角形的性质得到x=
,根据相似三角形的性质得到x= ![]() ,过C作CE∥x轴交抛物线与E,则CE=4,设抛物线与x轴交于F,B,则B(2+
,过C作CE∥x轴交抛物线与E,则CE=4,设抛物线与x轴交于F,B,则B(2+ ![]() ,0),于是得到结论;(3)解方程组得到D(﹣1,28得到Q(t,﹣12t+16)(﹣1≤t<2),①当﹣1≤t<0时,②当0<t<
,0),于是得到结论;(3)解方程组得到D(﹣1,28得到Q(t,﹣12t+16)(﹣1≤t<2),①当﹣1≤t<0时,②当0<t< ![]() 时,③当
时,③当 ![]() <t<2时,求得二次函数的解析式即可得到结论.
<t<2时,求得二次函数的解析式即可得到结论.
【考点精析】本题主要考查了二次函数的性质和二次函数的最值的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a才能正确解答此题.