题目内容
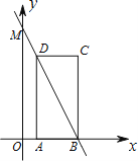
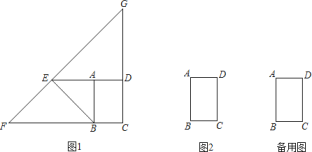
【题目】在矩形ABCD中,AB=3,AD=2,点E是射线DA上一点,连接EB,以点E为圆心EB长为半径画弧,交射线CB于点F,作射线FE与CD延长线交于点G.
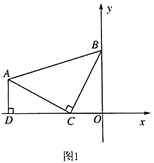
(1)如图1,若DE=5,则∠DEG=______°;
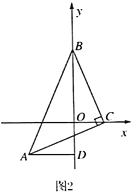
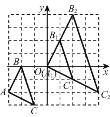
(2)若∠BEF=60°,请在图2中补全图形,并求EG的长;
(3)若以E,F,B,D为顶点的四边形是平行四边形,此时EG的长为______.
【答案】(1)45;(2)见解析,EG=4+2![]() ;(3)2
;(3)2![]()
【解析】
(1)由题意可得AE=AB=3,可得∠AEB=∠ABE=45°,由矩形的性质可得AD∥BC,可得∠AEB=∠EBF=45°,∠EFB=∠GED,结合等腰三角形的性质,即可求解;
(2)由题意画出图形,可得∠F=∠5=60°,可得∠6=∠G=30°,由直角三角形的性质可得AE=![]() ,DE=2+
,DE=2+![]() ,由直角三角形的性质可得EG的长;
,由直角三角形的性质可得EG的长;
(3)由平行四边形的性质可得EF=BD,ED=BF,由等腰三角形的性质可得AE=AD=2,由勾股定理可求EF=BE=![]() ,由EH∥CG∥BM,H是BF的中点,B是HC的中点,即可求解.
,由EH∥CG∥BM,H是BF的中点,B是HC的中点,即可求解.
(1)∵DE=5,AB=3,AD=2,
∴AE=AB=3,
∴∠AEB=∠ABE=45°,
∵四边形ABCD是矩形,
∴AD∥CB,
∴∠AEB=∠EBF=45°,∠EFB=∠GED,
∵EF=EB,
∴∠EFB=∠EBF=45°,
∴∠GED=45°,
故答案为:45;
(2)如图1所示.
∵四边形ABCD是矩形,
∴∠1=∠2=∠3=∠ABF=∠C=90°.
∵∠4=60°,EF=EB,
∴∠F=∠5=60°.
∴∠6=∠G=30°,
∴AE=![]() BE.
BE.
∵AB=3,
∴根据勾股定理可得:AE2+32=(2AE)2,解得:AE=![]() ,
,
∵AD=2,
∴DE=2+![]() ,
,
∴EG=2DE =4+2![]() ;
;
(3)如图2,连接BD,过点E作EH⊥FC,延长BA交FG于点M,
∵四边形EDBF是平行四边形,
∴EF=BD,ED=BF,
∵EF=BE,
∴EB=BD,且AB⊥DE,
∴AE=AD=2,
∴BF=DE=4,
∵EB=![]() =
=![]() ,
,
∴EF=![]() ,
,
∵EF=BE,EH⊥FC,
∴FH=BH=2=BC,
∴CH=4,
∵EH⊥BC,CD⊥BC,AB⊥BC,
∴EH∥CG∥BM,
∵H是BF的中点,B是HC的中点,
∴E是FM的中点,M是EG的中点,
∴EG═2EF=2![]()
故答案为:2![]()

 导学全程练创优训练系列答案
导学全程练创优训练系列答案