题目内容
【题目】在平面直角坐标系
中，存在抛物线
以及两点
．
(1)求该抛物线的顶点坐标；(用含
的代数式表示)
(2)若该抛物线经过点
，求此抛物线的表达式；
(3)若该抛物线与线段
有公共点，结合图象，求的取值范围．
【答案】（1）
；（2）：
或
；（3）
或
.
【解析】
（1）根据题意将抛物线的一般解析式化为顶点式即可得出抛物线的顶点坐标；
（2）根据题意将
代入求出m的值即可求得该抛物线的表达式；
（3）根据题意分m≥0，m＜0两种情形，分别构建不等式解决问题即可．
解：（1）∵抛物线解析式为：
，
∴顶点坐标为：.
（2）∵抛物线经过点，
∴
，解得
，
所以该抛物线的表达式为：或.
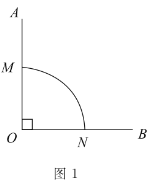
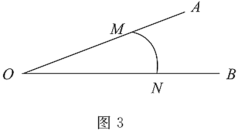
（3）当m≥0时，如图1中，
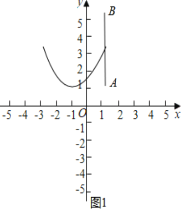
观察图象可知：
，
∴
且
，
解得．
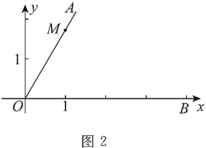
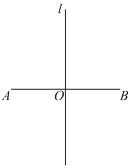
当m＜0时，如图2中，
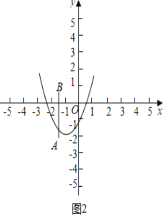
观察图象可知：，
∴m2+2m≥0且m2+2m-2≤0，
解得，
综上所述，满足条件的m的值为：或．
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案【题目】疫情期间，阿里巴巴“爱心助农”计划全面启动，集合天猫、淘宝、聚划算、饿了么、盒马、阿里乡村事业部等，组成了线上线下农产品销售的全域网络，通过这次爱心助农，很多农产品从滞销转变为脱销，以下是某淘宝商家在电商平台上推出的
．猕猴桃、
．芒果这两种水果，其销售信息如下表：
品种 | 销售信息 |
| 5所以内（包含5斤），每斤8元；超过5斤，则超出部分打8折 |
| 3斤以内（包含3斤），每斤10元；超出3斤，所有芒果打9折 |
（1）小佳购买
斤猕猴桃，付款
元，请写出与的函数关系式；
（2）若小佳购买10斤猕猴桃，小欣购买8斤芒果，比较谁的花费更低？
【题目】北京某超市按月订购一种酸奶，每天的进货量相同．根据往年的销售经验，每天需求量与当天最高气温（单位：℃）有关．为了确定今年六月份的酸奶订购计划，对前三年六月份的最高气温及该酸奶需求量数据进行了整理、描述和分析，下面给出了部分信息．
a．酸奶每天需求量与当天最高气温关系如表：
最高气温t（单位：℃） | 20≤t＜25 | 25≤t＜30 | 30≤t≤40 |
酸奶需求量（单位：瓶/天） | 300 | 400 | 600 |
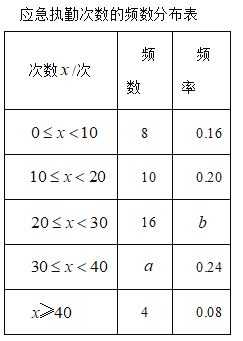
b.2017年6月最高气温数据的频数分布统计表如表（不完整）：
2017年6月最高气温数据的频数分布表：
分组 | 频数 | 频率 |
20≤t＜25 | 3 | |
25≤t＜30 | m | 0.20 |
30≤t＜35 | 14 | |
35≤t≤40 | 0.23 | |
合计 | 30 | 1.00 |
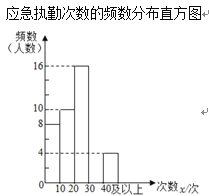
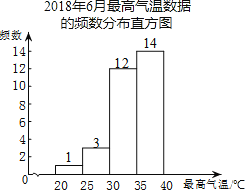
c.2018年6月最高气温数据的频数分布直方图如图：
d.2019年6月最高气温数据如下（未按日期顺序）：
25 26 28 29 29 30 31 31 31 32 32 32 32 32 32
33 33 33 33 33 34 34 34 35 35 35 35 36 36 36
根据以上信息，回答下列问题：
（1）m的值为 ；
（2）2019年6月最高气温数据的众数为 ，中位数为 ；
（3
（4）已知该酸奶进货成本每瓶4元，售价每瓶6元，未售出的酸奶降价处理，以每瓶2元的价格当天全部处理完．
①2019年6月这种酸奶每天的进货量为500瓶，则此月这种酸奶的利润为 元；
②根据以上信息，预估2020年6月这种酸奶订购的进货量不合理的为 ．
A．550瓶/天
B．600瓶/天
C．380瓶/天
