题目内容
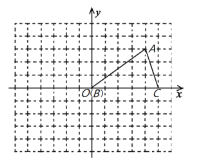
【题目】如图，在平面直角坐标系内，小正方形网格的边长为1个单位长度，
的三个顶点的坐标分别为
，
，
．
（1）画出将向上平移2个单位长度，再向左平移5个单位长度后得到的
；
（2）画出将绕点
按顺时针方向旋转90°得到的
；
（3）在
轴上存在一点
，满足点到点
与点
的距离之和最小，请直接写出点的坐标．
【答案】（1）答案见解析；（2）答案见解析；（3）
．
【解析】
（1）先分别将A、B、C三点向上平移2个单位长度，再向左平移5个单位长度得到
，然后连接
、
、
即可；
（2）根据题意，先将边OC和OA绕点
顺时针方向旋转90°得到
、
，然后连接
即可；
（3）连接
交x轴于点P，根据两点之间线段最短即可得出此时点
到点
与点
的距离之和最小，然后利用待定系数法求出直线的解析式，从而求出点P 的坐标．
解：（1）先分别将A、B、C三点向上平移2个单位长度，再向左平移5个单位长度得到，然后连接、、，如图所示，
即为所求；
（2）先将边OC和OA绕点顺时针方向旋转90°得到、，然后连接，如图所示，
即为所求；
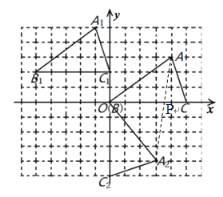
（3）连接交x轴于点P，根据两点之间线段最短，即可得出此时点到点与点的距离之和最小，
由平面直角坐标系可知：点A的坐标为（4,3），点的坐标为（3，-4）
设直线的解析式为y=kx＋b
将A、的坐标代入，得
解得：
∴直线的解析式为y=7x－25
将y=0代入，得
∴点P的坐标为．
练习册系列答案
智能训练练测考系列答案
相关题目
