Question

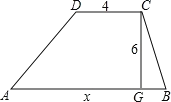
【题目】如图，AC是某市环城路的一段，AE，BF，CD都是南北方向的街道，其与环城路AC的交叉路口分别是A，B，C经测量东方家具城D位于点A的北偏东45°方向，点B的北偏东30°方向上，AB=2km，∠DAC=15°，求C、D之间的距离（结果保留根号）．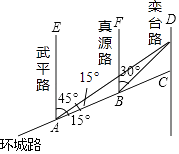

Answer 1

【答案】解：∵由题意可得∠EAD=45°，∠FBD=30°，

又∵∠DAC=15°，

∴∠EAC=60°，

∵AE∥BF，

∴∠FBC=∠EAB=60°，

∴∠DBC=30°，

∴∠BDA=∠DBC﹣∠DAB=30°﹣15°=15°，

∴∠BDA=∠DAB，

∴AB=DB=2km，

∴∠ADB=15°，

∴∠DBC=∠ADB+∠DAC=15°+15°=30°；

过B作BO⊥DC，交其延长线于点O，

在Rt△DBO中，BD=2，∠DBO=60°，

∴DO=2×sin60°= ，BO=2×cos60°=1．

在Rt△CBO中，∠CBO=30°，CO=BOtan30°= ，

∴CD=DO﹣CO= ﹣ = （km）．

即C，D之间的距离 km．

【解析】通过作垂线把特殊角放到直角三角形Rt△DBO、Rt△CBO中，利用平行线的性质，转化同位角得到∠CBO=30°，∠DBO=60°，进而 DO、CO，二者之差即可求出CD.