Question

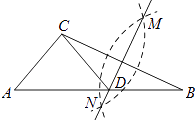
【题目】如图，已知△ABC，AB=BC，以AB为直径的圆交AC于点D，过点D的⊙O的切线交BC于点E．若CD=5，CE=4，则⊙O的半径是（ ）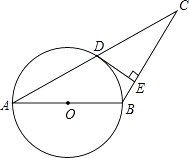

A.3
B.4
C.
D.

Answer 1

【答案】D
【解析】解：如图1，连接OD、BD，

，

∵AB是⊙O的直径，

∴∠ADB=90°，

∴BD⊥AC，

又∵AB=BC，

∴AD=CD，

又∵AO=OB，

∴OD是△ABC的中位线，

∴OD∥BC，

∵DE是⊙O的切线，

∴DE⊥OD，

∴DE⊥BC，

∵CD=5，CE=4，

∴DE= ，

∵S△BCD=BDCD÷2=BCDE÷2，

∴5BD=3BC，

∴ ，

∵BD2+CD2=BC2，

∴ ，

解得BC= ，

∵AB=BC，

∴AB= ，

∴⊙O的半径是；

．

故答案为：D．

连接OD、BD，根据圆周角定理得出∠ADB=90°，然后根据等腰三角形的三线合一得出AD=CD，进而推出OD是△ABC的中位线，从而得出OD∥BC，根据切线的性质定理及勾股定理得出DE的长，然后利用面积法得出5BD=3BC，再根据勾股定理得出方程求出BC的长，进而得出答案。