题目内容
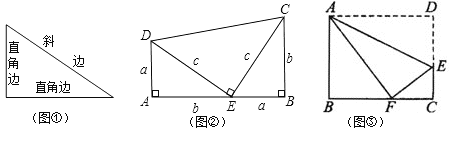
【题目】如图,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F,若∠C=30°,DF=2,求BD的长.

【答案】6.
【解析】
根据已知利用AAS判定△ABD≌△ACE,则AD=AE,∠B=∠C,因为AB=AC,可得BE=CD,再利用AAS判定△BEF≌△CDF,则BF=CF,BD=DF+CF,根据含30°的直角三角形的性质可得CF=2DF,即可求解.
解:∵AB=AC,BD⊥AC于D,CE⊥AB于E,
∴∠ADB=∠AEC=90°,∠BAD=∠CAE,
∴△ABD≌△ACE.
∴AD=AE,∠B=∠C,
∵AB = AC,
∴AC-AD=AB-AE.
∴BE=CD
又∵∠B=∠C,∠EFB=∠DFC,
∴△BEF≌△CDF,
∴BF=CF,则BD=DF+CF,
∵BD⊥AC于D,∠C=30°,DF=2,
∴CF=2DF=4,
∴BD=DF+CF=2+4=6.

练习册系列答案
相关题目