题目内容
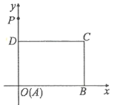
【题目】如图1,四边形ABCD内接于⊙O,AC为⊙O的直径,AC与BD交于点E,且AE=AB.
(1)DA=DB,求证:AB=CB;
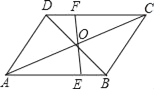
(2)如图2,△ABC绕点C逆时针旋转30°得到△FGC,点A经过的路径为![]() ,若AC=4,求图中阴影部分面积S;
,若AC=4,求图中阴影部分面积S;
(3)在(2)的条件下,连接FB,求证:FB为⊙O的切线.

【答案】(1)证明见解析;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)欲证明AB=BC,只要证明∠BAC=∠ACB即可;
(2)设AB的延长线交FG于M,连接CM,在BC上取一点N,使得CN=NM.证明Rt△CBM≌Rt△CGM,可得∠NCM=∠NMC=15°,从而∠MNB=30°,设BM=a,则MN=CN=2a,BN=![]() a,由2a+
a,由2a+![]() a=2
a=2![]() ,可求出BM的长,然后根据三角形面积公式计算即可;
,可求出BM的长,然后根据三角形面积公式计算即可;
(3)连接OB、BF、作FH⊥AC于H.只要证明四边形OBFH是矩形即可解决问题;
(1)证明:如图1中,

∵DA=DB,
∴∠DAB=∠DBA,
∵AE=AB,
∴∠AEB=∠ABE,
∴∠AEB=∠DAB,
∴∠EAD+∠ADE=∠EAD+∠EAB,
∴∠EAB=∠ADE,
∵∠ADE=∠ACB,
∴∠EAB=∠ACB,
∴AB=BC.
(2)如图2中,设AB的延长线交FG于M,连接CM,在BC上取一点N,使得CN=NM.

∵△ABC是等腰直角三角形,AC=4,
∴AB=BC=2![]() ,
,
∵BC=CG,CM=CM,
∴Rt△CBM≌Rt△CGM,
∴∠MCB=∠MCG=15°,
∵NC=NM,
∴∠NCM=∠NMC=15°,
∴∠MNB=30°,设BM=a,则MN=CN=2a,BN=![]() a,
a,
∴2a+![]() a=2
a=2![]() ,
,
∴a=4![]() ﹣2
﹣2![]() ,
,
∴S阴=2×![]() ×BM×BC=(4
×BM×BC=(4![]() ﹣2
﹣2![]() )×
)×![]() =16﹣8
=16﹣8![]() .
.
(3)如图2﹣1中,连接OB、BF、作FH⊥AC于H.

∵∠ACF=30°,∠FHC=90°,
∴FH=![]() CF=
CF=![]() AC=OA=OB,
AC=OA=OB,
∵BA=BC,OA=OC,
∴BO⊥AC,
∴FH∥OB,
∴四边形OBFH是平行四边形,
∵∠BOH=90°,
∴四边形OBFH是矩形,
∴∠OBF=90°,即OB⊥BF;
∴BF是⊙O的切线.