Question

【题目】如图，在△ABC中，如果BD,CE分别是∠ABC,∠ACB的平分线且他们相交于点P，设∠A=n°.

（1）求∠BPC的度数（用含n的代数式表示），写出推理过程.

（2）当∠BPC=125°时，∠A= .

（3）当n=60°时，EB=7，BC=12，DC的长为 .

Answer 1

【答案】（1）∠BPC=90°+n，推理过程见解析；（2）70°；（3）5.

【解析】

（1）根据角平分线的性质得∠ABC=2∠PBC，∠ACB=2∠PCB，再根据三角形内角和定理求得∠A=-180°+2∠BPC，即可求证∠BPC=90°+n；

（2）根据（1）可知∠BPC=90°+n，把∠BPC=125°代入原式求出n即为∠A的度数；

（3）当n=60°时，即可求出∠BPC=120°，作辅助线在CB上截取CG=CD，可证出△CPG≌△PCD（SAS），即可得出∠DPO=∠GPC，PD=PG，再可证出△BEP≌△BGP，即可得出BE=BG，即可求出DC．

解：（1）∵DB、CE分别为∠ABC，∠ACB的平分线，

∴∠ABC=2∠PBC，∠ACB=2∠PCB.

∵∠A=180°-(∠ABC+∠ACB)，

∴∠A=180°-2(∠PBC+∠PCB)，

∴∠A=180°-2(180°-∠BPC)，

∴∠A=-180°+2∠BPC，

∴2∠BPC=180°+∠A，

∴∠BPC=90°+∠A,

∴∠BPC=90°+n

（2）由（1）知∠BPC=90°+∠A

∴当∠BPC=125°时，∠A =2×（125°-90°）= 70°；

（3）在CB上截取CG=CD，连接GP，

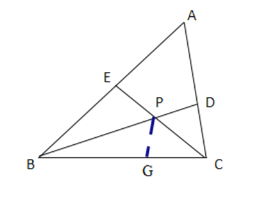
CE平分
∴∠GCP=∠PCD，
在△PCD和△PCG中，

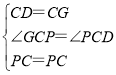
∴△PCD≌△CGP（SAS），

∴∠GPC=∠CPD，PG=PD，
由∠BPG+∠GPC=120°，
又∵∠BPG+2∠GPC=180°，
解得：∠BPG=∠GPC=∠FPC=60°
在△BEP和△BGP中，

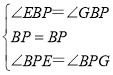
∴△BEP≌△BGP（ASA），
∴BE=BG，
∴CG=BC-BG=BC-BE=12-7=5

∴CD=CG=5．