题目内容
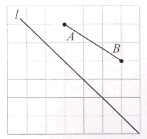
【题目】如图,在网格中,每个小正方形的边长都为1,网格中有两个格点![]() 、
、![]() 和直线
和直线![]() ,且
,且![]() 长为3.6.
长为3.6.
(1)求作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() .
.
(2)![]() 为直线
为直线![]() 上一动点,在图中标出使
上一动点,在图中标出使![]() 的值最小的
的值最小的![]() 点,且求出
点,且求出![]() 的最小值?
的最小值?
(3)求![]() 周长的最小值?
周长的最小值?
【答案】(1)见解析;(2)点P位置见解析,最小值为5;(3)8.6
【解析】
(1)根据题意作图即可
(2)连接BA1交直线l于点P,由两点间,线段最短即可确定点P的位置
(3)由(2)中求得点P的位置,即可得AB+AP+BP=AB+A1P+BP=AB+A1B
(1)如图,点A1即为所作点A关于直线l的对称点
(2)连接BA1交直线l于点P,连接AB,AP,则AP=A1P,由两点之间,线段最短可知,![]() 最短值为5,
最短值为5,
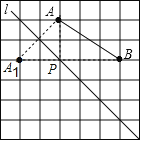
(3)由(2)可知,点P 即可使△ABP最小的位置
故△ABP周长的最小值为AB+AP+BP=AB+A1P+BP=3.6+A1B=3.6+5=8.6

练习册系列答案
相关题目