题目内容
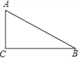
【题目】如图,两块大小不等的等腰直角三角形按图1放置,点![]() 为直角顶点,点
为直角顶点,点![]() 在
在![]() 上,将
上,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 角度
角度![]() ,连接
,连接![]() 、
、![]() .
.
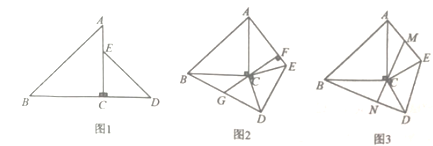
(1)若![]() ,则当
,则当![]()
![]() 时,四边形
时,四边形![]() 是平行四边形;
是平行四边形;
(2)图2,若![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() 是
是![]() 的中点;
的中点;
(3)图3,若点![]() 是
是![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() 时,四边形
时,四边形![]() 是平行四边形;(2)见解析;(3)见解析.
是平行四边形;(2)见解析;(3)见解析.
【解析】
(1)当AC∥DE时,因为AC=DE,推出四边形ACDE是平行四边形,利用平行四边形的性质即可解决问题.
(2)如图2中,作DM⊥FM于M,BN⊥FM交FM的延长线于N.利用全等三角形的性质证明BN=DM,再证明△BNG≌△DMG(AAS)即可解决问题.
(3)如图3中,延长CM到K,使得MK=CM,连接AK.KM.想办法证明△BCD≌△CAK(SAS),即可解决问题.
(1)解:如图1-1中,连接AE.
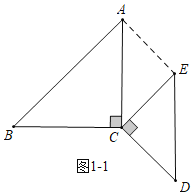
当AC∥DE时,∵AC=DE,
∴四边形ACDE是平行四边形,
∴∠ACE=∠CED,
∵CE=CD,∠ECD=90°,
∴∠CED=45°,
∴α=∠ACE=45°.
故答案为45.
(2)证明:如图2中,作DM⊥FM于M,BN⊥FM交FM的延长线于N.
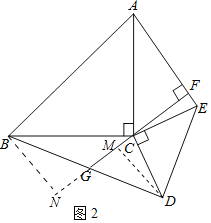
∵CF⊥AE,DM⊥FM,
∴∠CFE=∠CMD=∠ECD=90°,
∴∠ECF+∠CEF=90°,∠ECF+∠DCM=90°,
∴∠CEF=∠DCM,∵CE=CD,
∴△CFE≌△DMC(AAS),
∴DM=CF,
同法可证:CF=BN,
∴BN=DM,
∵BN⊥FM,
∴∠N=∠DMG=90°,
∵∠BGN=∠DGM,
∴△BNG≌△DMG(AAS),
∴BG=DG,
∴点G是BD的中点.
(3)证明:如图3中,延长CM到K,使得MK=CM,连接AK.KM.
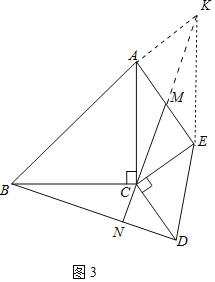
∵AM-ME,CM=MK,
∴四边形ACEK是平行四边形,
∴AK=CE=CD,AK∥CE,
∴∠KAC+∠ACE=180°,
∵∠ACE+∠BCD=180°,
∴∠BCD=∠KAC,
∵CA=CB,CD=AK,
∴△BCD≌△CAK(SAS),
∵∠ACK=∠CBD,
∵∠ACK+∠BCN=90°,
∴∠CBD+∠BCN=90°,
∴∠CNB=90°,
∴CN⊥BD.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案