Question

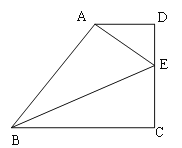
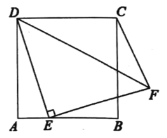
【题目】如图，已知正方形的边长为，点是边上-动点，连接，将绕点顺时针旋转到，连接，则的最小值是（ ）

A.B.C.D.

Answer 1

【答案】A

【解析】

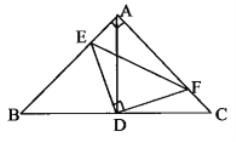
连接BF，过点F作FG⊥AB交AB延长线于点G，通过证明△AED≌△GFE（AAS），确定F点在BF的射线上运动；作点C关于BF的对称点C'，由三角形全等得到∠CBF=45°，从而确定C'点在AB的延长线上；当D、F、C'三点共线时，DF+CF=DC'最小，在Rt△ADC'中，AD=3，AC'=6，求出DC'=即可．

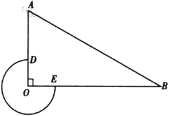
解：连接BF，过点F作FG⊥AB交AB延长线于点G，

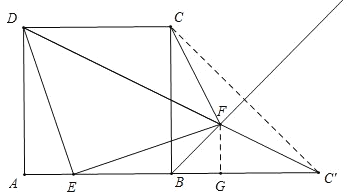
∵将ED绕点E顺时针旋转90°到EF，

∴EF⊥DE，且EF=DE，

∴△AED≌△GFE（AAS），

∴FG=AE，

∴F点在BF的射线上运动，

作点C关于BF的对称点C'，

∵EG=DA，FG=AE，

∴AE=BG，

∴BG=FG，

∴∠FBG=45°，

∴∠CBF=45°，

∴C'点在AB的延长线上，

当D、F、C'三点共线时，DF+CF=DC'最小，

在Rt△ADC'中，AD=3，AC'=6，
∴DC'=，

∴DF+CF的最小值为，

故选：A．