题目内容
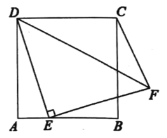
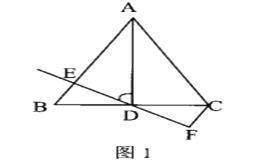
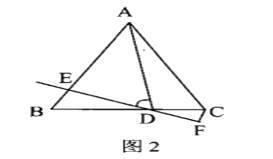
【题目】如图, 在![]() 中,
中,![]() ,
,![]() , 点
, 点![]() 为
为![]() 中点, 点
中点, 点![]() 在边
在边![]() 上, 连接
上, 连接![]() ,过点
,过点![]() 作
作
![]() 上
上![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 。下列结论:
。下列结论:
(1)![]() (2)
(2)![]() (3)
(3)![]() (4)
(4)![]()
其中正确的是__________(填写所有正确结论的序号)
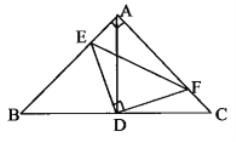
【答案】![]()
【解析】
由“ASA”可证△ADE≌△CDF,可得AE=CF,S△ADE=S△CDF,由等腰直角三角形的性质可判断(1),(3),由三角形的三边关系可判断(2),由三角形面积关系可判断(4).
∵AB=AC,∠BAC=90°,点D为BC中点,
∴BD=CD=AD=![]() BC,∠BAD=∠CAD=∠C=45°,AD⊥BC,BC=
BC,∠BAD=∠CAD=∠C=45°,AD⊥BC,BC=![]() AB,
AB,
∵DF⊥DE,
∴∠EDF=∠ADC=90°,
∴∠ADE=∠CDF,且AD=CD,∠BAD=∠C,
∴△ADE≌△CDF(ASA),
∴AE=CF,
∴BE+CF=BE+AE=AB,且BC=![]() AB,
AB,
∴BE+CF=![]() BC,故(1)正确;
BC,故(1)正确;
∵AE+AF≥EF,
∴AF+CF≥EF,
∴AC≥EF,
∴![]() AD≥EF,故(2)错误;
AD≥EF,故(2)错误;
∵△ADE≌△CDF,
∴S△ADE=S△CDF,
∴S四边形AEDF=S△ADF+S△CDF=S△ADC=![]() ×AD2,故(3)正确;
×AD2,故(3)正确;
∵S△AEF=![]() ×AE×AF,且AE+AF=AC,
×AE×AF,且AE+AF=AC,
∴当AE=AF时,S△AEF的最大值=![]() S△ABC,
S△ABC,
∴S△AEF≤![]() ,故(4)正确,
,故(4)正确,
故答案为:(1) (3) (4)

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目