题目内容
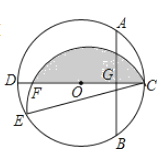
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 为半径作优弧
为半径作优弧![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .点
.点![]() 在优弧
在优弧![]() 上从点
上从点![]() 开始移动,到达点
开始移动,到达点![]() 时停止,连接
时停止,连接![]() .
.
(1)当![]() 时,判断
时,判断![]() 与优弧
与优弧![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)当![]() 时,求点
时,求点![]() 在优弧
在优弧![]() 上移动的路线长及线段
上移动的路线长及线段![]() 的长.
的长.
(3)连接![]() ,设
,设![]() 的面积为
的面积为![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.


备用图
【答案】(1)AM与优弧的相切(2)![]() 或
或![]() (3)
(3)![]()
【解析】
(1)根据勾股定理的得到∠AMO=90°即可得到![]() 与优弧
与优弧![]() 的相切;
的相切;
(2)根据题意分![]() 在直线
在直线![]() 的左侧和右侧两种情况讨论,用三角函数及相似三角形的性质进行求解;(3)根据题意作过点
的左侧和右侧两种情况讨论,用三角函数及相似三角形的性质进行求解;(3)根据题意作过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() 此时
此时![]() 的面积最大,过点
的面积最大,过点![]() 作
作![]() 于点
于点![]() ,即点
,即点![]() 与点
与点![]() 重合,此时
重合,此时![]() 的面积最小,分别求出
的面积最小,分别求出![]() 最大值与最小值即可求解.
最大值与最小值即可求解.
在![]() 中,
中,![]() ,
,![]() ,
,![]()
![]() .
.
(1)![]() 与优弧的相切;
与优弧的相切;
如图1,当![]() 时,
时,![]() ,
,![]() 且
且![]()
![]() 为直角三角形,
为直角三角形,![]() ,
,
![]() 点
点![]() 在
在![]() 上,
上,![]()
![]() 与优弧
与优弧![]() 的相切.
的相切.

(2)当![]() 时,第一种情况:如图 2所示,
时,第一种情况:如图 2所示,![]() 在直线
在直线![]() 的左侧;
的左侧;![]()
![]()
过点![]() 作
作![]() 于点
于点![]()
在![]() 中,
中,![]()
![]() ,
,![]() ,
,![]()
在![]() 中,据勾股定理可知
中,据勾股定理可知![]() .
.

第二种情况:如图 3所示,![]() 在直线
在直线![]() 的右侧;连接
的右侧;连接![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
在![]() 中,据勾股定理得:
中,据勾股定理得:![]()
由![]() 可知
可知![]() .
.
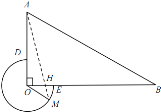
(3)如图4,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() 此时
此时![]() 的面积最大
的面积最大
在![]() 中,
中,![]() ,
,![]()
![]()
![]()
在![]() 中
中![]()
![]()
![]()

如图5,过点![]() 作
作![]() 于点
于点![]() ,即点
,即点![]() 与点
与点![]() 重合,此时
重合,此时![]() 的面积最小
的面积最小
在![]() 中
中
![]()
![]()
![]() .
.

练习册系列答案
相关题目
【题目】绿色无公害蔬菜基地有甲、乙两种植户,他们种植了![]() 两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植 | 种植 | 总收入(单位:元) |
甲 |
|
|
|
乙 |
|
|
|
说明:不同种植户种植的同类蔬菜每亩的平均收入相等;亩为土地面积单位
![]() 求
求![]() 两类蔬菜每亩的平均收入各是多少元?
两类蔬菜每亩的平均收入各是多少元?
![]() 某种植户准备租
某种植户准备租![]() 亩地用来种植
亩地用来种植![]() 两类蔬菜,为了使总收入不低于
两类蔬菜,为了使总收入不低于![]() 元且种植
元且种植![]() 类蔬菜的面积多于种植
类蔬菜的面积多于种植![]() 类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案;
类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案;
![]() 在
在![]() 的基础上,指出哪种方案使总收入最大,并求出最大值.
的基础上,指出哪种方案使总收入最大,并求出最大值.