Question

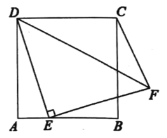
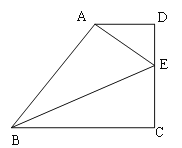
【题目】如图，在梯形中，∥，∠=90°，，

⑴求的长；

⑵若∠的平分线交于点，连结，求∠的正切值．

Answer 1

【答案】（1）4；（2）2

【解析】

(1) 过点A作AFBC垂足为F，得到BF的长度，在Rt△AFB中运用勾股定理即可得到AF的长度，利用AF=DC进而得到答案；

(2)先证明≌（SAS），根据全等三角形的性质得到∠AEB=∠CEB，运用勾股定理求解CE的长度即可得到答案；

解：（1）过点A作AFBC垂足为F，

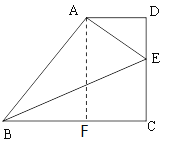
由题意得FC=AD=2，AF=CD，.

∵BC=5，

∴BF=5-2=3，

在Rt△AFB中：

（勾股定理），

即：

解得AF=4，

∴CD=4；

（2）由AB=BC，∠ABE=∠CBE，BE=BE，

得到≌（SAS），

∴∠AEB=∠CEB（全等三角形对应边相等），

∴AE=EC（全等三角形对应边相等），

设AE=EC=，

则DE=，

在Rt△ADE中，

，

解得，