题目内容
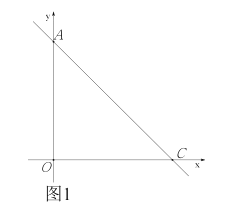
【题目】平面直角坐标系中,直线![]() 交坐标轴于点
交坐标轴于点![]() 、点
、点![]() 且
且![]() 面积为
面积为![]()
![]() 如图1,求
如图1,求![]() 的值;
的值;
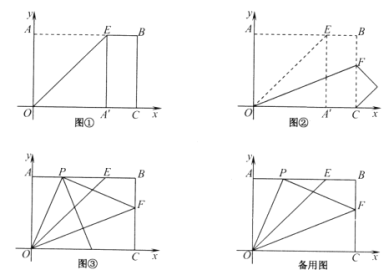
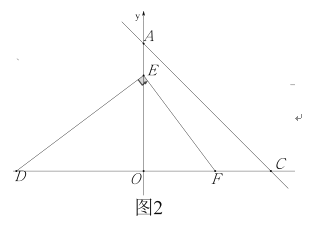
![]() 如图2,点
如图2,点![]() 在
在![]() 轴的负半轴上,
轴的负半轴上,![]() 在线段
在线段![]() 上,连
上,连![]() ,作
,作![]() 交线段
交线段![]() 于
于![]() , 若
, 若![]() 点纵坐标为
点纵坐标为![]() 长度为
长度为![]() ,求
,求![]() 与
与![]() 的函数关系式(不写自变量取值范围);
的函数关系式(不写自变量取值范围);
【答案】![]() ;
;![]() .
.
【解析】
(1)设A、B的坐标分别为(0,b)(b,0)且b>0,然后表示出OA和OB,然后用三角形面积公式求解即可;
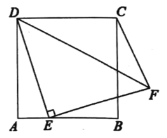
(2)由题意可得D、E、F的坐标分别为(-5,0)、(0,t)、(d,0),然后表示出DE2、EF2、DF2,最后根据勾股定理列式化简即可;
解:(1)设A、B的坐标分别为(0,b)(b,0)且b>0
则OA=b,OB=b
∵![]()
∴b=5或b=-5(舍去)
∴b=5;
(2)由题意可得(-5,0)、(0,t)、(d,0)
则DE2=25+t2,DF=(5+d)2=25+10d+ d2,EF= t2+ d2
∵![]()
∴DE2+EF2=DF2,即25+t2+t2+d2=25+10d+ d2
∴![]() ;
;

练习册系列答案
相关题目