Ő‚ńŅńŕ»›
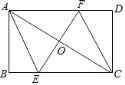
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨∑ĹłŮ÷Ĺ÷–√ŅłŲ–°’ż∑Ĺ–őĶńĪŖ≥§∂ľ «Ķ•őĽ1£¨°ųABCĶń»żłŲ∂•Ķ„∂ľ‘ŕłŮĶ„…Ō£¨ĹŠļŌňýłÝĶń∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶĹ‚īūŌ¬Ń–ő Ő‚£ļ
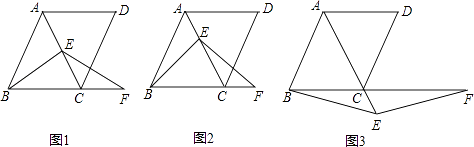
£®1£©Ĺę°ųABCŌÚ”“∆Ĺ“∆3łŲĶ•őĽ≥§∂»‘ŔŌÚŌ¬∆Ĺ“∆2łŲĶ•őĽ≥§∂»£¨Ľ≠≥ŲŃĹīő∆Ĺ“∆ļůĶń°ųA1B1C1£Ľ
£®2£©–ī≥ŲA1°ĘC1Ķń◊ÝĪÍ£Ľ
£®3£©Ĺę°ųA1B1C1»∆C1ńś Ī’Ž–ż◊™90°„£¨Ľ≠≥Ų–ż◊™ļůĶń°ųA2B2C1 £¨ «ů°ųA1B1C1–ż◊™Ļż≥Ő÷–…®ĻżĶń√śĽż£®ĹŠĻŻĪ£Ń۶–£©
°ĺīūįł°Ņ
£®1£©Ĺ‚£ļ»ÁÕľ£¨°ųA1B1C1ő™ňý◊ų£ļ
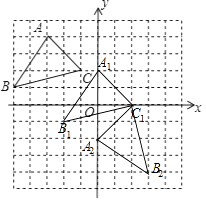
£®2£©Ĺ‚£ļA1£®0£¨2£©£¨C1£®2£¨0£©
£®3£©Ĺ‚£ļ»ÁÕľ£¨°ųA2B2C1ő™ňý◊ų£ļ

S°ųA1B1C=4°Ń3©Ā ![]() °Ń4°Ń1©Ā
°Ń4°Ń1©Ā ![]() °Ń2°Ń2©Ā
°Ń2°Ń2©Ā ![]() °Ń2°Ń3=5£¨
°Ń2°Ń3=5£¨
B1C1= ![]() =
= ![]() £¨
£¨
ňý“‘°ųA1B1C1–ż◊™Ļż≥Ő÷–…®ĻżĶń√śĽż=S°ųA1B1C1+S…»–őB1C1B2
= ![]() +5
+5
= ![]() ¶–+5
¶–+5
°ĺĹ‚őŲ°Ņ£®1£©°ĘņŻ”√Ķ„∆Ĺ“∆Ķń◊ÝĪÍŐō’ų–ī≥ŲA°ĘB°ĘCĶń∂‘”¶Ķ„A1°ĘB1°ĘC1Ķń◊ÝĪÍ£¨»Ľļů√ŤĶ„Ķ√ĶĹ°ųA1B1C1£Ľ
£®2£©łýĺ›∂‘”¶Ķ„÷ĪĹ”–ī≥ŲA1°ĘC1Ķń◊ÝĪÍľīŅ….
£®3£©ņŻ”√ÕÝłŮĶńŐōĶ„ļÕ–ż◊™Ķń–‘÷ £¨–ī≥ŲĶ„A1°ĘB1Ķń∂‘”¶Ķ„A2°ĘB2Ķń◊ÝĪÍ£¨‘Ú√ŤĶ„Ķ√ĶĹ°ųA2B2C1£¨‘ŔņŻ”√√śĽżĶńļÕ≤Óľ∆ň„≥ŲS°ųA1B1C£¨»Ľļůłýĺ›…»–őĶń√śĽżĻę Ĺ£¨ņŻ”√°ųA1B1C1–ż◊™Ļż≥Ő÷–…®ĻżĶń√śĽż=S°ųA1B1C1+S…»–őB1C1B2ĹÝ––ľ∆ň„ľīŅ…Ķ√ĶĹĹŠ¬Ř£ģ

 √Ż–£ŅőŐ√ŌĶŃ–īūįł
√Ż–£ŅőŐ√ŌĶŃ–īūįł°ĺŐ‚ńŅ°Ņ![]() ņ ∂Ń’Ŗ
ņ ∂Ń’Ŗ![]() ◊‘Ņ™≤•“‘ņī£¨“‘∆šļŮ÷ōĶńőńĽĮĶ◊‘ŐļÕł–»ňĶń»ňőń«ťĽ≥£¨ł–∂ĮŃň ż“‘“ŕľ∆ĶńĻŘ÷ŕ£¨‘ņ≥ōŌōń≥÷–—ßŅ™’Ļ°įņ ∂Ń°ĪĪ»»ŁĽÓ∂Į£¨ĺŇńÍľ∂
◊‘Ņ™≤•“‘ņī£¨“‘∆šļŮ÷ōĶńőńĽĮĶ◊‘ŐļÕł–»ňĶń»ňőń«ťĽ≥£¨ł–∂ĮŃň ż“‘“ŕľ∆ĶńĻŘ÷ŕ£¨‘ņ≥ōŌōń≥÷–—ßŅ™’Ļ°įņ ∂Ń°ĪĪ»»ŁĽÓ∂Į£¨ĺŇńÍľ∂![]() °Ę
°Ę![]() įŗłýĺ›≥ű»Ł≥…ľ®£¨łų—°≥Ų5√Ż—° ÷≤őľ”łī»Ł£¨ŃĹłŲįŗłų—°≥ŲĶń5√Ż—° ÷Ķńłī»Ł≥…ľ®
įŗłýĺ›≥ű»Ł≥…ľ®£¨łų—°≥Ų5√Ż—° ÷≤őľ”łī»Ł£¨ŃĹłŲįŗłų—°≥ŲĶń5√Ż—° ÷Ķńłī»Ł≥…ľ®![]() ¬ķ∑÷ő™100∑÷
¬ķ∑÷ő™100∑÷![]() »ÁÕľňý ĺ£ģ
»ÁÕľňý ĺ£ģ
∆Ĺĺý ż | ÷–őĽ ż | ÷ŕ ż | |
ĺŇ | 85 | 85 | |
ĺŇ | 80 |
![]() łýĺ›Õľ ĺŐÓ–īĪŪłŮ£Ľ
łýĺ›Õľ ĺŐÓ–īĪŪłŮ£Ľ
![]() ĹŠļŌŃĹįŗłī»Ł≥…ľ®Ķń∆Ĺĺý żļÕ÷–őĽ ż£¨∑÷őŲńńłŲįŗľ∂Ķńłī»Ł≥…ľ®ĹŌļ√£Ľ
ĹŠļŌŃĹįŗłī»Ł≥…ľ®Ķń∆Ĺĺý żļÕ÷–őĽ ż£¨∑÷őŲńńłŲįŗľ∂Ķńłī»Ł≥…ľ®ĹŌļ√£Ľ
![]() »ÁĻŻĻś∂®≥…ľ®ĹŌő»∂®įŗľ∂ §≥Ų£¨ń„»Ōő™ńńłŲįŗľ∂ń‹ §≥Ų£ŅňĶ√ųņŪ”…£ģ
»ÁĻŻĻś∂®≥…ľ®ĹŌő»∂®įŗľ∂ §≥Ų£¨ń„»Ōő™ńńłŲįŗľ∂ń‹ §≥Ų£ŅňĶ√ųņŪ”…£ģ