题目内容
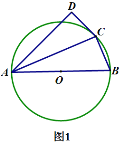
【题目】如图1,![]() 是
是![]() 的外接,
的外接,![]() 是直径,
是直径,![]() 是
是![]() 外一点且满足
外一点且满足![]() ,连接
,连接![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,
,![]() ,求直径
,求直径![]() 的长;
的长;
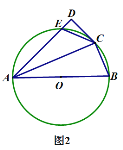
(3)如图2,当![]() 时,
时,![]() 与
与![]() 交于
交于![]() 点,试写出
点,试写出![]() 、
、![]() 、
、![]() 之间的数量关系并证明.
之间的数量关系并证明.
【答案】(1)见详解;(2)5;(3)![]() ,证明见详解
,证明见详解
【解析】
(1)连接OC,由OB=OC知∠OCB=∠B,结合∠DCA=∠B得∠DCA=∠OCB,再由AB是直径知∠ACB=90°,据此可得∠DCA+∠ACO=∠OCB+∠ACO=90°,从而得证;
(2)先利用勾股定理求得AC=2![]() ,再证△ADC∽△ACB得
,再证△ADC∽△ACB得![]() ,据此求解可得;
,据此求解可得;
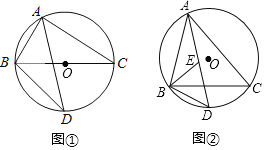
(3)连接BE,在AC上截取AF=BC,连接EF..由AB是直径、∠DAB=45°知∠AEB=90°,据此得△AEB是等腰直角三角形,AE=BE,再证△ECB≌△EFA得EF=EC,据此可知△FEC是等腰直角三角形,从而得出![]() ,从而得证.
,从而得证.
解:(1)证明:连接OC.
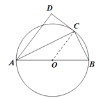
∵OB=OC
∴∠OCB=∠B
∵∠DCA=∠B
∴∠DCA=∠OCB
∵AB是直径
∴∠ACB=90
∴∠DCA+∠ACO =∠OCB+∠ACO=90,
即∠DCO=90,
∴CD是⊙O的切线
(2)∵AD⊥CD,CD=2,AD=4.
∴![]() ,
,
由(1)可知∠DCA=∠B,∠D=∠ACB=90
∴△ADC∽△ACB
∴![]()
∴![]()
∴AB=5.
(3)![]() ,
,
如图2,连接BE,在AC上截取AF=BC,连接EF.

∵AB是直径,∠DAB=45
∴∠AEB=90
∴△AEB是等腰Rt△
∴AE=BE
又∵∠EAC=∠EBC,
∴△ECB≌△EFA
∴EF=EC,∵∠ACE=∠ABE=45
∴△FEC是等腰Rt△
∴![]()
∴![]() .
.

练习册系列答案
相关题目